Différentes écritures d’un nombre complexe

L'interprétation géométrique des nombres complexes va permettre de donner de nouvelles formes d'écriture.

Dans tout ce qui suit, le plan est rapporté à un repère orthonormé $(0\;; \vec u \;,\vec v)$
À tout complexe $z=x+iy$, avec $x$ et $y$ réels, on associe le point M du plan de coordonnées $(x\;; y)$.
On dit que z est l'affixe de M, ou que z est l'affixe du vecteur $\overrightarrow{OM}$.

$|z|=\sqrt{x^2+y^2}=OM$
Remarque : un module est un réel positif ou nul.

Les points M d'affixe z et M' d'affixe $\bar z$ sont symétriques par rapport à l'axe des abscisses.

Dans le plan complexe, soit $z$ non nul, affixe du point $M$.
On appelle argument de $z$ toute mesure en radians de l'angle $\widehat{(\overrightarrow {u}\;; \overrightarrow{OM})}$.
Tout nombre complexe non nul a donc une infinité d'arguments (définis à $2\pi$ près).

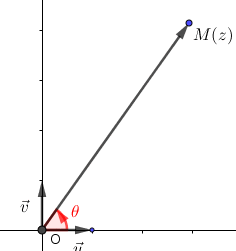
Dans cet exemple, $\arg(z)=\theta (2\pi)$

Tout point M(z) du plan, distinct de l'origine, est repéré par sa distance à l'origine $OM$ et par l'angle $\widehat{(\overrightarrow {u} \;; \overrightarrow{OM})}$.

On peut donc écrire :
$\boxed{z=x+iy=|z|\left(\cos (\theta)+i \sin (\theta)\right)}$

Cette écriture $z=|z|\left(\cos (\theta)+i \sin (\theta)\right)$ s'appelle l'écriture ou la forme trigonométrique du complexe z. On l'écrit également $z=[|z|\;; \theta]$.

Une autre écriture de ce même complexe est l'écriture exponentielle.

On retiendra que l'écriture $\text e^{\text i\theta}$ n'est rien d'autre que $\cos (\theta)+i \sin (\theta)$.

z réel non nul équivaut à dire $arg(z)=0 +k\pi \;, k\in \textbf Z$

z imaginaire pur non nul équivaut à dire $arg(z)=\dfrac{\pi}{2}+k\pi \;, k\in \textbf Z$

Exemple 1 : Donner la forme trigonométrique du complexe $z=-2\left(\cos \left(\dfrac{\pi}{4}\right)+i\sin \left(\dfrac{\pi}{4}\right)\right)$ et placer le point M d'affixe z dans le plan complexe.

Le réel -2 étant négatif, ceci n'est pas une écriture trigonométrique.

$z=-2\left(\cos \left(\dfrac{\pi}{4}\right)+i\sin \left(\dfrac{\pi}{4}\right)\right)=2\left((-1)\cos \left(\dfrac{\pi}{4}\right)+i(-1)\sin \left(\dfrac{\pi}{4}\right)\right)$

Or on sait que $\cos \left(\dfrac{5\pi}{4}\right)=-\cos \left(\dfrac{\pi}{4}\right)$ et $\sin \left(\dfrac{5\pi}{4}\right)=-\sin \left(\dfrac{\pi}{4}\right)$,
donc la forme trigonométrique de z est : $z=2\left(\cos \left(\dfrac{5\pi}{4}\right)+i\sin \left(\dfrac{5\pi}{4}\right)\right)$.

Sa forme exponentielle est donc : $z=2\,\text e^{\,\text i\,\frac{5\pi}{4}}$

On donne $z=\sqrt 3+\text i$. Donner sa forme trigonométrique.

Le module d'un nombre complexe $z = x + \text{i}y$ est donné par : $|z| = \sqrt{x^2 + y^2}$.
Ici, $x = \sqrt{3}$ et $y = 1$. Donc :
$|z| = \sqrt{(\sqrt{3})^2 + 1^2} = \sqrt{3 + 1} = \sqrt{4} = 2$.

Mettons $2$ en facteur. $z$ s'écrit $z=2\left(\dfrac{\sqrt 3}{2}+\text i \dfrac 12\right)$
Or : La forme trigonométrique d’un complexe $z$ est donnée par :
$z = |z| \left( \cos(\theta) + \text{i}\sin(\theta) \right)$.
Ainsi, un argument de $z$ est $\theta = \dfrac{\pi}{6}$.

Conclusion
La forme trigonométrique de $z$ est :
$z = 2\left(\cos\left(\dfrac{\pi}{6}\right) + \text{i}\sin\left(\dfrac{\pi}{6}\right)\right)$.

Merci à Malou pour avoir contribué à l'élaboration de cette fiche.