Des fonctions affines en physique, économie ou EMC

Cette fiche regroupe des exemples classiques faisant intervenir des fonctions affines.

I. Un exemple en physique : les échelles Celsius et Fahrenheit

Enoncé : 

En France, les températures sont mesurées en degrés Celsius (°C).
Les pays anglo-saxons utilisent le degré Fahrenheit (°F).
La fonction qui a une température  $x$  en degrés Celsius, associe cette température  $y$  en degrés Fahrenheit est une fonction affine.

1) On sait que 0°C équivaut à 32 °F et que 100 °C équivallent à 212 °F.
Déterminer l'expression de la fonction $g$ telle que $y=g(x)$.

2) a. Le thermomètre indique 15°C, calculer la valeur correspondante en °F.
     b. Le thermomètre indique 50°F, calculer la valeur correspondante en °C.

3) a. Entre 25 °C et 75 °F quelle est la température la plus élevée ?
     b. Entre -20 °C et 0 °F quelle est la valeur la plus basse ?

4) Calculer la température à laquelle les deux échelles donnent la même valeur.

5) Quelle est la fonction affine $f$ qui à une température $y$ en degrés Fahrenheit associe la température équivalente en degrés Celsius ?

Solution : 

L'énoncé stipule que $g$ est une fonction affine de $x$. On a donc : $y=g(x)=ax+b$ avec $a$ et $b$ réels.

1) $g(0)=32$ et $g(100)=212$.

$g(0)=32 \Longleftrightarrow 32=a\times 0+b$. On trouve :

$\boxed{b=32}$

$g(100)=212 \Longleftrightarrow 212=a\times 100 +32$. On trouve : 

$180=a\times 100$ soit $\boxed{a= 1,8}$.

Conclusion : $g(x)=1,8 x+32$

2) a. On nous donne la température en degrés Celsius qui est $15$. Ceci est donc la valeur de $x$. Remplaçons : 

$g(15)=1,8\times 15+32=59$ 

Conclusion : $15$ °C correspondent à $59$ °F.

   b. On nous donne la température en degrés Fahrenheit qui est $50$. On cherche l'antécédent de $50$ par la fonction affine $g$. Pour cela il suffit de résoudre l'équation : $50=1,8\times x+32$.

$50-32=1,8\times x$

$18 = 1,8\times x$

$\dfrac{18}{1,8}=x$ soit $\boxed{x=10}$.

Conclusion : $50$ °F correspondent à $10$ °C.

3) a. Si $x=25$, alors $g(x)= 1,8\times 25+32=77$. Donc $25$°C correspond à $77$°F. La température la plus élevée est donc $25$°C.

    b. Si $x=-20$ alors $g(x)=1,8\times (-20)+32=-4$. Donc $-20$°C correspond à $-4$°F. 

Conclusion : La température la plus basse est $-20$°C.

4) Soit $t$ la température (en degré Celsius) à laquelle les deux échelles donnent la même valeur. Cela signifie que $t$ a pour image $g(t)$ qui doit être égal à $t$.

$g(t)=t \Longleftrightarrow 1,8\times t +32= t$

${\phantom{g(t)=t}\Longleftrightarrow 0,8\,t=-32}$ en retranchant $t-32$ aux deux membres de l'égalité.

${\phantom{g(t)=t}\Longleftrightarrow t=-40}$ en divisant les deux membres par $0,8$.

Conclusion : les deux échelles donnent la même température pour $-40$°C (et donc également $-40$°F).

5) On sait que $y=1,8\,x+32$. Je retranche $32$ aux deux membres. 

$y-32=1,8\,x$ soit $\dfrac{y-32}{1,8}=x$. On en déduit que : 

$x=\dfrac{1}{1,8}\,y-\dfrac{32}{1,8}$

$x=\dfrac{5}{9}\,y-\dfrac{160}{9}$

Conclusion : la fonction affine $g$ est définie sur $\textbf R$ par 

$\boxed{g(y)=\dfrac{5}{9}\,y-\dfrac{160}{9}}$

II. Un exemple en économie : offre, demande et point d'équilibre

L'offre et la demande désignent respectivement la quantité d'un bien ou d'un service que les acteurs du marché sont prêts à vendre ou à acheter à un prix donné.
On note $f$ la fonction définie sur R par $f(x)=20x-25$ et $g$ la fonction définie sur R par $g(x) = -5x + 100$. 

Une étude de marché a permis d'établir que les fonctions $f$ et $g$ modélisent respectivement l'offre et la demande d'un produit sur l'intervalle $[1\;;\;n]$ où $n$ est le prix de vente pour lequel la demande est nulle.

• $f(x)$ est la quantité, exprimée en milliers d'articles, que les producteurs sont prêts à vendre au prix unitaire de $x$ euros.
• $g(x)$ est la quantité, exprimée en milliers d'articles, que les consommateurs sont prêts à acheter au prix unitaire de $x$ euros.     

1) Quel est le sens de variation des fonctions $f$ et $g$ ? Interpréter ces résultats (on rappelle que $f$ et $g$ sont respectivement les fonctions d'offre et de demande).

2) Déterminer $n$.

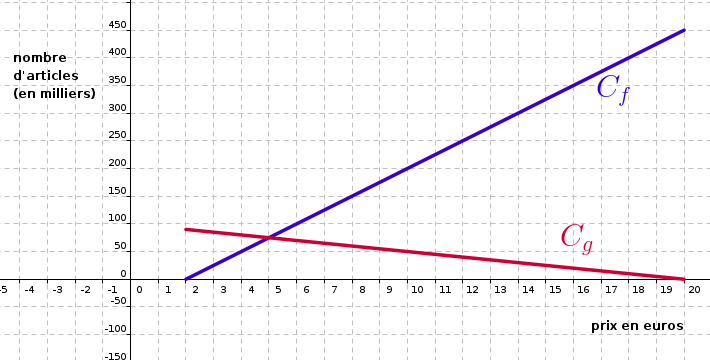
3) Tracer les courbes représentatives des fonctions $f$ et $g$ sur $[2\;;\;n]$ dans un repère du plan.

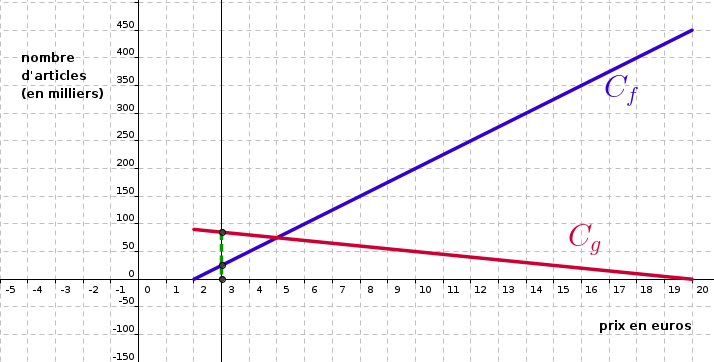
4) Comparer graphiquement l'offre et la demande pour un prix de vente de 3 euros.

5) Déterminer graphiquement le prix de vente à partir duquel le nombre d'articles offerts sur le marché par les producteurs sera supérieur à 100 000. Quel problème cela pose-t-il à l'entreprise ?

6) On dit que le marché est à l'équilibre lorsque, pour un même prix, la quantité offerte est égale à la quantité demandée.
Déterminer graphiquement le prix d'équilibre et la quantité associée.

7) Déterminer par le calcul le prix d'équilibre. Vérifier que le résultat est cohérent avec le résultat de la question 6).

Solution :

1) $f(x)=20x-25$ , le coefficient directeur de la droite représentatiove de cette fonction affine est $20$ donc $f$ est croissante.

Pour $g$, on a $g(x)=-5x+100$, $-5$ est négatif, donc $g$ est décroissante. 

Le fabricant désire vendre le plus d'articles possibles au meilleur prix, mais si le prix $x$ augment les acheteurs eux vont acheter moins d'articles. 

2) La demande est nulle pour $n$ défini par $g(n)=0$. 

$g(n)=0\Longleftrightarrow -5n+100=0$ soit $n=20$. La demande est nulle lorsque le prix atteint $20$ euros.

3)

4) Traçons la droite d'équation $x=3$ sur la représentation graphique. 

Pour $x=3$ euros, la demande (en rouge) est supérieure à l'offre (en bleu). 

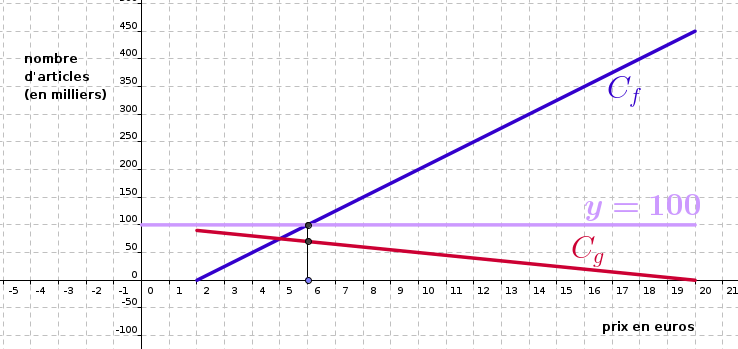
5) Le prix de vente à partir duquel le nombre d'articles offerts sur le marché par les producteurs sera supérieur à 100 000 (soit 100 milliers d'articles) est lu sur l'axe des abscisses.

Graphiquement, il semble que ce prix soit de $6$ euros, mais on lit également sur le graphique que l'offre est alors supérieure à le demande, d'où un problème pour le fabriquant.

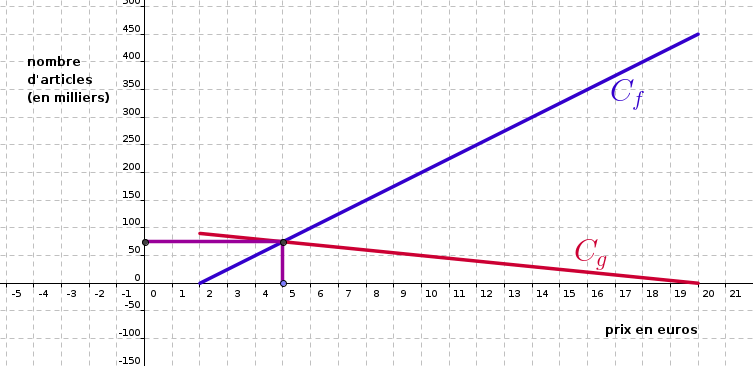
6) 

Le prix d'équilibre semble être $5$ euros, pour un nombre d'articles qui serait de environ $75$ milliers.

7) Vérifions par le calcul.

Le point déquilibre est obtenu à l'intersection de deux courbes. 

Résolvons l'équation $f(x)=g(x)$.

$f(x)=g(x)\Longleftrightarrow 25x-50=-5x+100$

${\phantom{f(x)=g(x)}\Longleftrightarrow 30x=150}$ en ajoutant $5x+50$ aux deux membres.

${\phantom{f(x)=g(x)}\Longleftrightarrow x=5}$ en divisant par $30$ les deux membres. 

Le prix d'équilibre est bien $5$ euros comme lu graphiquement.

Lorsque $x=5$, $f(5)=25\times 5-50=75$. Le nombre d'articles correspondant au prix d'équilibre est de $75\,000$.

III. Un exemple en EMC

On peut lire sur le site du gouvernement français le barème de l'impôt sur le revenu applicable en 2024.

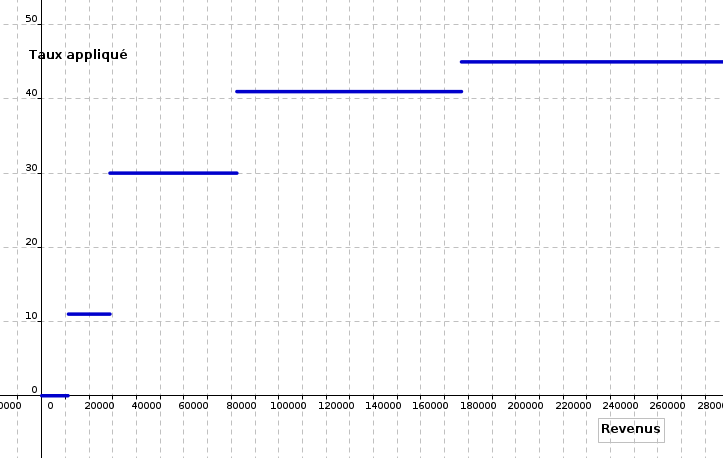
Ces pourcentages appliqués peuvent être représentés graphiquement par une fonction affine par morceaux. En voici une représentation : 

Exemple : Un célibataire a un revenu net imposable de $30\,000$ euros. Quel va être le montant de ses impôts ? 

Sur la tranche $[0\;;\;11\,294]$, il ne paie rien.

Sur la tranche $[11\,295\;;\;28\,797]$, il paie $11\%$ soit $\dfrac{11}{100}\times (28\,797 - 11\,295)$ soit $1925,22$ euros.

Au delà, soit sur la tranche $[28\,798\;;\;30\,000]$, il paie $30\%$ soit $\dfrac{30}{100}\times (30\,000 - 28\,798)$ soit $360,60$ euros.

Au total, il paiera : $1\,925,22 + 360,60=2\,285,82$ euros.