I- Intégrale d'une fonction continue positive
Soient deux réels tels que et soit une fonction continue et positive sur l'intervalle . On se propose de déterminer l'aire délimitée par la courbe représentative de la fonction notée , l'axe des abscisses et les droites d'équations . Autrement dit, cette aire représente l'ensemble des points dont les coordonnées vérifient : .
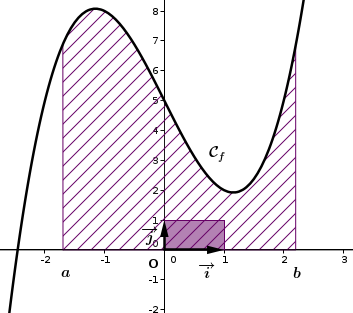
Commençons par présenter l'unité d'aire dans un repère, c'est l'une des notions fondamentales de ce cours :
Définition : Unité d'aire L'unité d'aire dans un repère est l'aire du rectangle où , elle est souvent notée
Exemples : Dans le cas d'un repère orthonormé tel que Dans la figure précédente, on a
Définition : Intégrale d'une fonction continue positive Soit une fonction continue et positive sur l'intervalle . On appelle l'intégrale de la fonction de à et on note l'aire délimitée par la courbe représentative de la fonction , l'axe des abscisses et les droites d'équations en unité d'aire .
Exemple : Soit la fonction linéaire définie sur par: représentée graphiquement sur deux repères différents :
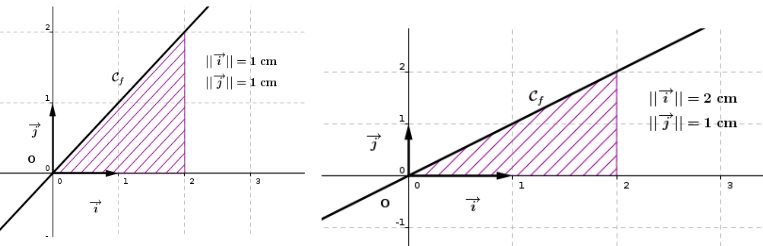
L'aire hachurée en est dans les deux cas égale à:
Par contre, en , les deux aires ne seront plus égales parce que les deux repères n'ont pas la même :
L'unité d'aire dans le cas de la première figure : , ce qui veut dire que dans ce cas:
L'unité d'aire dans le cas de la seconde figure : , donc:
Remarque : La variable dans la notation est dite muette, elle intervient dans le calcul comme on va le voir dans les paragraphes suivants mais pas dans le résultat final, on peut la remplacer par n'importe quelle autre variable:
Remarque : La variable dans la notation est dite muette, elle intervient dans le calcul comme on va le voir dans les paragraphes suivants mais pas dans le résultat final, on peut la remplacer par n'importe quelle autre variable:
La question suivante se pose, qu'en est-il des fonctions continues de signe quelconque ?
II- Intégrale d'une fonction continue de signe quelconque
Définition : Intégrale d'une fonction continue négative
Soit une fonction continue et négative sur l'intervalle . On appelle l'intégrale de la fonction de à et on note l'opposé de l'aire délimitée par la courbe représentative de la fonction , l'axe des abscisses et les droites d'équations en unité d'aire (appelée aussi l'aire algébrique).
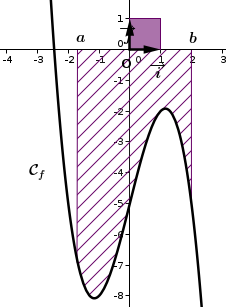
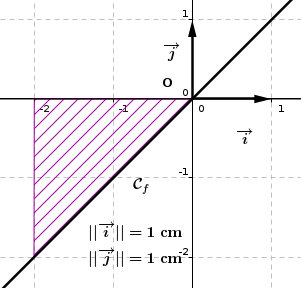
Exemple : Reprenons l'exemple précédent de la fonction linéaire définie sur par : , notons l'aire hachurée.
III. Intégrale d'une fonction continue de signe quelconque
Soit une fonction continue sur l'intervalle . On appelle l'intégrale de la fonction de à et on note la somme des aires algébriques délimitées par la courbe représentative de la fonction , l'axe des abscisses et les droites définissants les sous-intervalles dans lesquels la fonction est de signe constante.
Autrement dit, est égale à la différence entre : La somme des aires délimitées par la courbe représentative de et l'axe des abscisses quand est positive. Et la somme des aires délimitées par la courbe représentative de et l'axe des abscisses lorsque est négative.
Autrement dit, est égale à la différence entre : La somme des aires délimitées par la courbe représentative de et l'axe des abscisses quand est positive. Et la somme des aires délimitées par la courbe représentative de et l'axe des abscisses lorsque est négative.
Illustration graphique :
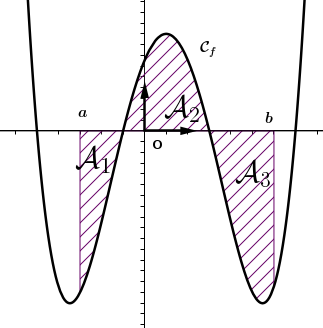
Exemple : La fonction linéaire définie sur par: . Trouver
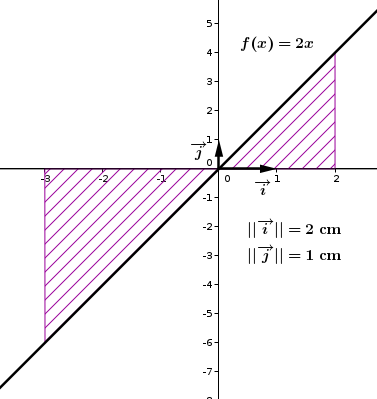
On remarque que : Sur l'intervalle , la fonction f est négative et la partie de l'intégrale demandée sur cet intervalle notée se trouve en dessous de l'axe des abscisses, elle est donc négative. Sur l'intervalle , la fonction f est positive et la partie de l'intégrale demandée sur cet intervalle notée se trouve en dessus de l'axe des abscisses, elle est donc positive.
Dans tous les exemples vus précédemment, on s'est contenté de présenter des fonctions affines simples pour lesquelles le calcul des aires est facile à faire en appliquant des résultats basiques de géométrie. Par contre, pour les fonctions avec des représentations graphiques non linéaires (des courbes géométriquement indéterminées), la méthode "géométrique" de calcul d'aire devient quasiment impossible. Comment calculer l'intégrale de ces fonctions alors?
IV. Méthode des rectangles
Bien souvent, on ne connaît pas de primitive de la fonction proposée, et on peut par exemple utiliser la méthode des rectangles pour approcher l'aire sous la courbe. Nous allons appliquer cette méthode sur la fonction carré, tout en sachant que dans ce cas particulier, nous saurions calculer l'aire exacte.
Pour estimer l'aire sous la courbe sur l'intervalle , on divise cet intervalle en sous-intervalles de même longueur . Sur chaque sous-intervalle, on construit un rectangle de hauteur égale à la valeur de la fonction en un point choisi, soit l'extrémité gauche par exemple, ou l'extrémité droite, suivant que l'on désire une valeur inférieure à l'aire, une valeur supérieure, en fonction également de la croissance de la courbe étudiée.
Pour estimer l'aire sous la courbe sur l'intervalle , on divise cet intervalle en sous-intervalles de même longueur . Sur chaque sous-intervalle, on construit un rectangle de hauteur égale à la valeur de la fonction en un point choisi, soit l'extrémité gauche par exemple, ou l'extrémité droite, suivant que l'on désire une valeur inférieure à l'aire, une valeur supérieure, en fonction également de la croissance de la courbe étudiée.
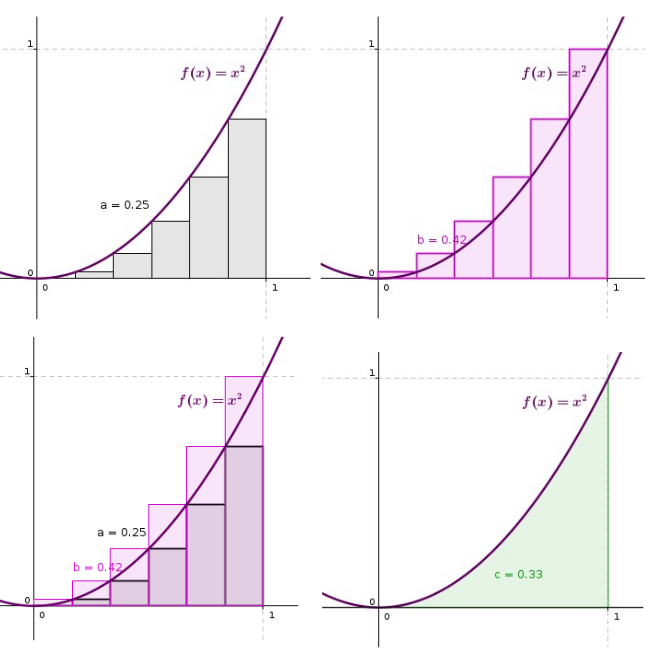
Par cette approche graphique, on trouve que l'aire sous la courbe est comprise entre et . Plus le nombre d'intervalles sera grand, plus l'encadrement sera meilleur. Ici, l'intervalle a été divisé en .
En réalité les expressions de et sont respectivement :
et
et
Si nous prenons , nous obtenons cet encadrement : .
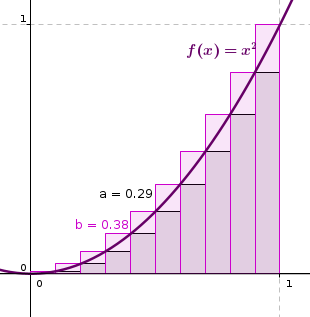
Et lorsque devient très grand, on obtient
.
Merci à Panter et à Malou pour avoir participé à l'élaboration de cette fiche.
.
Merci à Panter et à Malou pour avoir participé à l'élaboration de cette fiche.
