I. Fonctions convexes ou concaves : définitions
Soient une fonction définie et dérivable sur un intervalle de , et sa courbe représentative dans un repère orthogonal du plan.
La fonction est convexe sur lorsque située au-dessus de chacune de ses tangentes.
La fonction est concave sur lorsque est située au-dessous de chacune de ses tangentes.
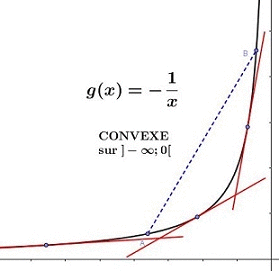
Exemples : fonction carré sur , et fonction inverse sur .

Exemple de la fonction inverse :

Propriété
Soient une fonction définie et dérivable sur un intervalle , et sa courbe représentative dans un repère orthogonal.
La fonction est convexe sur lorsque est située au-dessous de toutes ses cordes.
La fonction est concave sur lorsque est située au-dessus de toutes ses cordes.
Exercice d'application :
Trace à main levée la courbe représentative des fonctions suivantes et précise leur convexité sur les intervalles précisés :
, sur
sur
sur
Solution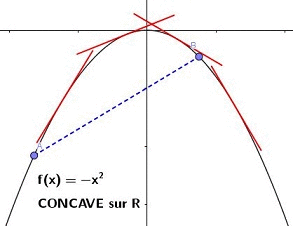
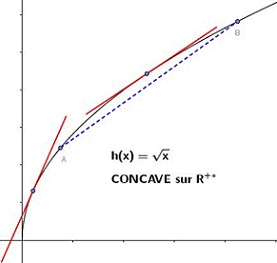
II- Point d'inflexion
Définition
Soit une fonction définie et dérivable sur un intervalle , et sa courbe représentative.
S'il existe un point de , tel que traverse la tangente en ce point, alors est un point d'inflexion.
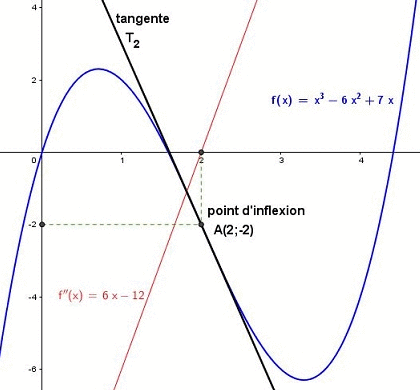
Exemple : la fonction cube , définie sur , admet l'origine du repère pour point d'inflexion.
La représentation graphique de la fonction traverse sa tangente en , d'équation .
On remarque que la fonction change de convexité en son point d'inflexion : sur est concave ; sur est convexe.
Propriétés
Soient une fonction définie et dérivable deux fois sur un intervalle , son graphe, et .
Si la dérivée change de sens de variation en , alors admet un point d'inflexion en , et le point de la courbe a pour coordonnées .
Si la dérivée seconde s'annule en et change de signe, alors admet un point d'inflexion en .
En ce point d'inflexion, la fonction change de convexité.
Exemple :
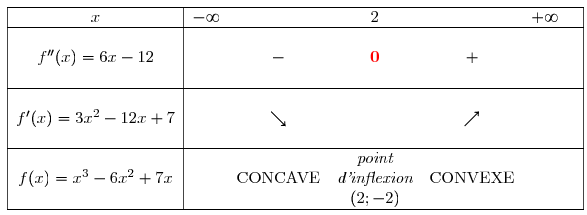
Soit la fonction définie sur par
Étudier la convexité de et préciser les éventuels points d'inflexion.
Solution :
La fonction est dérivable, donc continue sur .
On peut résumer l'étude de la convexité de dans le tableau suivant :
Explications :
Signe de : la dérivée seconde s'annule en .
Variation de : la dérivée change de sens de variation en .
Convexité de : la fonction change de convexité, et il existe un point d'inflexion en .
Vérification graphique : on constate que la courbe de traverse sa tangente en .
Merci à Carita et Malou pour avoir participé à l'écriture de cette contribution.