Variations d'une fonction

Lorsqu’on étudie une fonction, on s’intéresse notamment à ses variations : sur quel(s) intervalle(s) est-elle croissante ou décroissante ? Quels sont ses minimums ? ses maximums ?

I Monotonie sur un intervalle

Repère
À noter

Si f est croissante, les images de a et b sont rangées dans le même ordre que a et b.

Si f est décroissante, les imagesde a et b sont rangées dans l’ordre inverse de a et b.

Dire qu’une fonction f est croissante sur un intervalle I signifie qu’elle conserve l’ordre. Autrement dit, quels que soient les nombres a et b de I :

a < b ⇒ f(a) ⩽ f(b)

Dire qu’une fonction f est décroissante sur un intervalle I signifie qu’elle inverse l’ordre. Autrement dit, quels que soient les nombres a et b de I :

a < b ⇒ f(a) ⩾ f(b)

Dire qu’une fonction f est monotone sur un intervalle I signifie qu’elle est soit croissante, soit décroissante sur I.

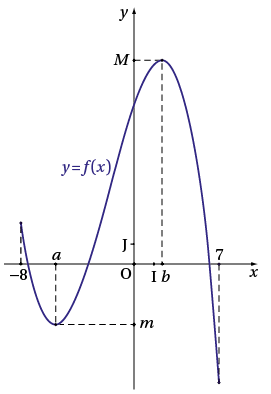
Exemple : En parcourant de gauche à droite la courbe ci-contre représentant la fonction f, on constate que :

• f est décroissante sur [–8 ; a] et sur [b ; 7] ;

• f est croissante sur [a ; b] ;

• La fonction f est monotone sur chacun des intervalles précédents (mais elle n’est pas monotone sur [–8 ; 7]).

II Tableau de variation

On résume les variations d’une fonction dans un tableau de variation. On y indique aussi, le cas échéant, les maximums et les minimums de la fonction.

Soit f une fonction définie sur un intervalle I, et a et b deux points de I.

• Dire que f a un minimum en a sur I signifie que pour tout x ∈ I :  f(a) ⩽ f(x) 

• Dire que f a un maximum en b sur I signifie que pour tout x ∈ I :  f(x) ⩽ f(b) 

Exemple : La fonction f représentée ci-dessus a un minimum en a sur [–8 ; b] car f(a) = m et m ⩽ f(x) pour tout x de cet intervalle.

Exploiter le tableau de variation d’une fonction

En utilisant le tableau de variation ci-dessous, déterminer :

a. les intervalles sur lesquels f est monotone ;

b. le signe de f(x) pour tout x de [–3 ; 11] ;

c. le nombre d’antécédents de 3.

Repère
ConseilS

a. Interprétez les flèches : ↗ signifie que la fonction f est croissante et ↘ signifie qu’elle est décroissante.

b. Analysez les maximums et les minimums sur chaque intervalle où la fonction est monotone. Ils sont indiqués aux extrémités des flèches.

c. Repérez où se trouve le nombre 3 sur les flèches de variation et déduisez-en les positions des antécédents.

solution

a. f est monotone sur les intervalles [–3 ; 1] et [5 ; 11] (où elle est croissante) et [1 ; 5] (où elle est décroissante).

b. Pour tout x de [–3 ; 1] : f(x) ⩾ 0. En effet, sur cet intervalle, la plus petite valeur de f(x) est 0.

Pour tout x de [1 ; 5] : f(x) ⩾ 2 et pour tout x de [5 ; 11] : f(x) ⩾ 2.

En effet, sur chacun de ces intervalles, la plus petite valeur de f(x) est 2.

On en conclut que pour tout x de [–3 ; 11], f(x) ⩾ 0.

c. La lecture du tableau de variation complété suivant fournit la réponse.

Le nombre 3 a trois antécédents : a compris entre –3 et 1, b compris entre 1 et 5, et c compris entre 5 et 11.