Pour montrer que deux droites sont parallèles, on peut utiliser la réciproque du théorème de Thalès ou le fait qu’elles soient perpendiculaires à une même troisième droite… Désormais on pourra également montrer ce parallélisme par le calcul.
I Parallélisme
1 Cas général
On considère deux droites d et d′ dont les équations cartésiennes respectives sont ux + vy + w = 0 et u′x + v′y + w′ = 0.
Les droites d et d′ sont parallèles si et seulement si uv′ – u′v = 0.
Preuve. Les vecteurs et sont des vecteurs directeurs de d et d′. Les droites d et d′ sont donc parallèles si et seulement si ces deux vecteurs sont colinéaires, autrement dit, si et seulement si leur déterminant est égal à 0. Or le déterminant de ces deux vecteurs est précisément (– v)u′ – u(– v′) = – vu′ + uv′.
2 Cas des équations réduites
Théorème. Deux droites d’équations respectives y = mx + p et y = m′x + p′ sont parallèles si et seulement si m = m′.
Preuve. L’équation de d s’écrit aussi mx – y + p = 0, donc le vecteur est un vecteur directeur de d, de même, est un vecteur directeur de d′. Donc ces deux droites sont parallèles si et seulement si 1 × m – 1 × m′ = 0, soit m – m′ = 0.
Remarque : On en déduit que deux droites d’équations respectives y = mx + p et y = m′x + p′ sont sécantes si et seulement si m ≠ m′.
II Condition d’alignement de trois points
Théorème. Trois points distincts A, B, C sont alignés si et seulement si les droites (AB) et (AC) ont la même pente ou s’ils ont tous trois la même abscisse.
Preuve. Si les points A, B et C sont alignés, alors les droites (AB) et (AC) sont confondues, donc elles ont le même coefficient directeur, ou les points ont la même abscisse.
Réciproquement :
• Supposons que les droites (AB) et (AC) aient le même coefficient directeur. Alors ces deux droites sont parallèles d’après le théorème précédent. Comme elles ont le point A en commun, elles sont confondues, ce qui prouve que les points A, B et C sont alignés.
• Si les trois points ont la même abscisse, alors ils sont alignés sur une droite verticale.
Méthode
Déterminer le point d’intersection de deux droites
a. Démontrer que les droites d et d′ d’équations respectives : y = 3x – 1 et y = –2x + 4 sont sécantes.
b. Calculer les coordonnées de leur point d’intersection M.
c. Tracer les deux droites dans un repère.Repère
d. Résoudre graphiquement le système .
Conseils
a. Considérez les coefficients directeurs des deux droites.
b. Exprimez le fait que les coordonnées de M satisfont les deux équations.
c. Choisissez deux points pour chacune des droites.solution
d. Utilisez les équations des deux droites précédentes.
a. La droite d a pour coefficient directeur 3 et la droite d′ a pour coefficient directeur– 2. Ces deux coefficients sont distincts. Donc les deux droites sont sécantes.
b. Les coordonnées (x ; y) de M vérifient chacune des deux équations. Donc on a simultanément y = 3x – 1 et y = –2x + 4. On en déduit que : 3x – 1 = –2x + 4, soit 5x = 5 et x = 1. L’abscisse du point M est donc égale à 1.Pour trouver son ordonnée, on choisit l’une des deux équations. On trouve y = 3 × 1 – 1 = 2 avec l’équation de d. Le point M a donc pour coordonnées (1 ; 2).
À noterOn trouve évidemment aussi y = –2 × 1 + 4 = 2 avec l’équation de d′.
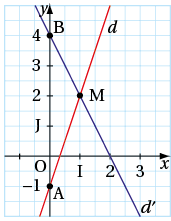
c. Pour tracer d, on choisit les points A(0 ; –1) et M(1 ; 2). Pour tracer d′, on choisit B(0 ; 4) et M(1 ; 2).À noter
d. Le système est équivalent au système .Un système de deux équations à deux inconnues peut se résoudre graphiquement ou par le calcul.
Graphiquement, les solutions du système sont les coordonnées du point d’intersection des droites y = 3x – 1 et y = –2x + 4. On a vu que ce sont les coordonnées du point M. En conclusion, on peut dire que le système a un couple solution unique qui est x = 1 et y = 2.