Coefficient directeur

Le coefficient directeur, également appelé pente ou pente de la droite, est un concept mathématique utilisé en géométrie analytique pour mesurer l'inclinaison d'une droite dans un plan cartésien. Il représente le rapport entre le déplacement vertical (l'ordonnée) et le déplacement horizontal (l'abscisse) entre deux points distincts de la droite.

I Généralités

Théorème. Soit A et B deux points de coordonnées respectives (xA ; yA) et (xB ; yB). Dans le cas où la droite (AB) n’est pas parallèle à l’axe des ordonnées, son coefficient directeur est égal à :

Repère
À noter

Une droite admet un coefficient directeur à la condition exclusive qu’elle ne soit pas parallèle à l’axe des ordonnées.

$\frac{y_{\text{B}}–y_{\text{A}}}{x_{\text{B}}–x_{\text{A}}}$

Preuve. Le coefficient directeur de la droite qui a pour équation y = mx + p est le nombre m. On sait que yA = mxA + p et yB = mxB + p. Donc :

$\frac{y_{\text{B}}–y_{\text{A}}}{x_{\text{B}}–x_{\text{A}}}\text{=}\frac{m{x}_{\text{B}}+p–(m{x}_{\text{A}}+p)}{x_{\text{B}}–x_{\text{A}}}=\frac{m{x}_{\text{B}}–m{x}_{\text{A}}}{x_{\text{B}}–x_{\text{A}}}=\frac{m(x_{\text{B}}–x_{\text{A}})}{x_{\text{B}}–x_{\text{A}}}=m$.

II Propriétés des coefficients directeurs (ou pentes)

Repère
À noter

Intuitivement, la pente est nulle sur un terrain plat.

Comment trouver le coefficient directeur d'une droite dont on connaît la représentation graphique

La pente d’une droite horizontale (parallèle à l’axe des abscisses) est nulle. D’ailleurs son équation est de la forme y = p.

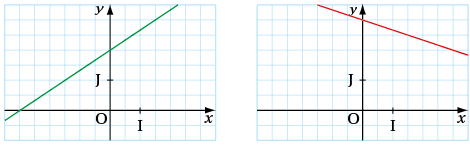
Dans un repère, on parcourt une droite de gauche à droite, dans le sens de lecture usuel.

• Si la droite « monte » (figure de gauche), alors la pente est positive ; elle représente une fonction affine croissante.

• Si la droite « descend » (figure de droite), alors la pente est négative ; elle représente une fonction affine décroissante.

Comment trouver le coefficient directeur d'une droite dont on connaît deux points

On peut trouver graphiquement la pente d’une droite sans en avoir l’équation. Il suffit de connaître deux points sur la droite (voir).

Méthode

Trouver graphiquement la pente d’une droite

1.
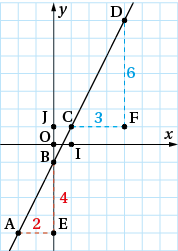
a. Déterminer graphiquement la pente de la droite tracée ci-contre dans le repère (O, I, J), à l’aide des points A et B d’une part, et C et D d’autre part.

b. La pente d’une route s’exprime en pourcentage.

Le panneau ci-dessous signale que, sur cette route, pour 100 m de déplacement horizontal (théorique), on s’élève (ou on descend) verticalement de 10 m.

Quel rapport y a-t‑il entre la pente d’une droite et la pente d’une route ?

2. Déterminer l’équation de la droite (AB).

Repère
Conseils

1. Visualisez les déplacements horizontaux et verticaux exprimés par xB – xA et yB – yA. De même pour les points C et D.

2. On connaît m, il suffit de trouver p.

solution

1.
a. Comme la droite « monte », on peut déjà savoir que le coefficient directeur est positif.

D’autre part, yB – yA est la distance EB et xB – xA est la distance AE.

$\frac{y_B–y_A}{x_B–x_A}=\frac{\text{EB}}{\text{EA}}$. La pente de la droite, calculée à l’aide des points A et B, est égale à $\frac{4}{2}$ c’est-à-dire 2.

On trouve, de même, $\frac{y_D–y_C}{x_D–x_C}=\frac{\text{FD}}{\text{FC}}=2$.

b. Le panneau de signalisation est trompeur car, en réalité, la pente de 10 % se mesure comme celle d’une droite, c’est-à-dire à l’aide d’un triangle rectangle et non d’un triangle quelconque.

La route ci-contre a une pente de :

$\frac{v}{h}=\frac{1}{10}=\frac{10}{100}=10\%$.

2. L’équation est de la forme y = 2x + p. L’ordonnée à l’origine est yB = –1. L’équation cherchée est donc y = 2x – 1.