I. Fonctions circulaires (rappels)
1) Rappels
Pour tout nombre réel a ; sin2a + cos2a = 1.
Si cos a ≠ 0, tan a=sin acos a.
2) Valeurs particulières

3) Figures relatives aux angles associés
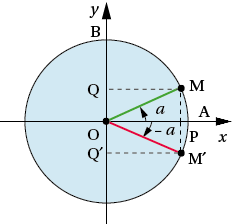
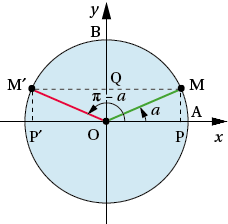
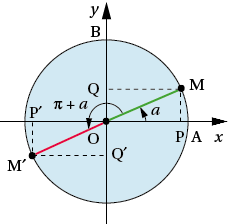
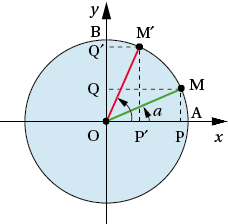
Plutôt que de chercher à retenir directement les formules suivantes, il vaut mieux apprendre à les retrouver sur une figure. Sur les quatre figures suivantes : les coordonnées de M donnent sin a et cos a, les coordonnées de M’ donnent le sinus et le cosinus des angles associés en fonction de sin a et cos a.
Réels opposés : a et – a.
Pour tout nombre réel a :
sin (– a) = – sin a ;
cos (– a) = cos a.
On peut retenir que la fonction sinus est impaire et que la fonction cosinus est paire.
Réels dont la somme est π : a et π – a.
Pour tout nombre réel a :
sin (π – a) = sin a ;
cos (π – a) = – cos a.
Réels dont la différence est π : a et π + a.
Pour tout nombre réel a :
sin (π + a) = – sin a ;
cos (π + a) = – cos a.
Réels dont la somme est π2 : a et π2−a.
Le cosinus de l’un est le sinus de l’autre.
Pour tout nombre réel a :
sin (π2−a)=cos a ;
cos (π2−a)=sin a.
II. L’ensemble des nombres complexes (rappels)
1) Forme algébrique d’un nombre complexe
En Première, nous avons admis l’existence d’un nouvel ensemble des nombres, noté ℂ, appelé ensemble des nombres complexes.
z = a + bi, où a et b sont deux nombres réels et i tel que i2 = – 1, est la forme algébrique du nombre complexe z.
Remarque
Les nombres complexes sont très utilisés en électricité ; afin d’éviter des confusions avec l’intensité i d’un courant électrique, un nombre complexe est alors noté a + bj au lieu de a + bi qui demeure l’écriture utilisée habituellement en mathématiques.
2) Opérations sur les nombres complexes
On peut définir dans ℂ une addition et une multiplication pour lesquelles les règles de calcul sont les mêmes que dans ℝ, avec i2 = – 1.
3) Opérations sur les nombres complexes
z¯=a−bi est le nombre complexe conjugué de z = a + bi.
Exemple
Le nombre complexe conjugué de z=6+23i est z¯=6−23i.
Mettre sous la forme a + bi l’inverse d’un nombre complexe.
Exemples
• On se propose de mettre sous la forme a + bi le nombre complexe z3=13+2i, inverse de z1 = 3 + 2i.
z3=3−2i(3+2i)(3−2i), z3=3−2i9−4i2, z3=3−2i9+4, z3=313−213i.
• En procédant comme pour z3, démontrer que :
2−3i−4−i=517+1417i
On multiplie numérateur et dénominateur par le conjugué du dénominateur.
On utilise les mêmes identités remarquables que dans ℝ. Remplacer i2 par – 1.
Propriétés
Pour tous nombres complexes z1 et z2 :
• z1+z2¯=z1¯+z2¯ ; • z1×z2¯=z1¯×z2¯ ; • z1≠0, ( 1 ¯z1)=1z1¯ ; • z2≠0, (z1z2)¯ =z1¯z2¯.
III. Représentation géométrique d’un nombre complexe
Le plan est muni du repère orthonormé direct (O ; u→, v→).
L’image du nombre complexe z = a + bi est le point M de coordonnées (a, b).
L’affixe du point M de coordonnées (a, b) est le nombre complexe z = a + bi.
Le vecteur image du nombre complexe z = a + bi est le vecteur w→=au→+bv→.
L’affixe du vecteur w→=au→+bv→ est le nombre complexe z = a + bi.
Si A et B sont deux points d’affixes respectives zA et zB, l’affixe du vecteur AB→ est : zB – zA.
Exemple
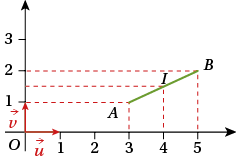
Soit les points A et B d’affixes zA = 3 + i et zB = 5 + 2i. A et B sont donc les points de coordonnées (3, 1) et (5, 2).
L’affixe du milieu I du segment [AB] est zI=zA+zB2.
zI=3+i+5+2i2=8+3i2=82+32i=4+32i. Donc I a pour coordonnées (4, 32). L’affixe du vecteur AB→ est zAB→=zB–zA=2+i.
IV. Module et argument d’un nombre complexe
1) Forme algébrique d’un nombre complexe
Le module du nombre complexe z = a + bi est le nombre |z|=a2+b2.
Exemples
• Le module de 1 + 2i est : 12+22=5. • Le module de – 3i est : 02+(− 3)2=3.
• Le module de – 3 + j est : 10. • Le module de − 12 est : 12.
Si M est l’image de z, |z|=OM.
Pour tous points A et B d’affixes zA et zB, AB=|zB–zA|.
Le module d’un produit est le produit des modules.
Si |z′|≠0, le module du quotient zz′ est le quotient des modules.
Un argument d’un nombre complexe non nul z = a + bi est un nombre réel θ tel que : cos θ=aa2+b2=az.sin θ=ba2+b2=bz..
Notation : un argument de z se note : argz.
Un argument de z est une mesure de l’angle orienté (u→, OM→).
Exemple
On considère le nombre complexe z=2+i6.
Le module de z est |z|=(2)2+(6)2, |z|=8, |z|=2×4, |z|=22.
Notons θ un argument de z.
cos θ=2z=222, cos θ=12 ; sin θ=6z=3×222, sin θ=32.
On lit dans le tableau des valeurs particulières du paragraphe ➀ B que θ=π3 (+ k2π). Un argument de z est π3.
Il faut savoir retrouver rapidement ces valeurs remarquables avec la calculatrice.
2) Forme trigonométrique
Soit z = a + bi un nombre complexe non nul, avec |z|=r et arg z = θ.
Une forme trigonométrique de z est : z = r(cos θ + i sin θ).
Exemple
On considère le nombre complexe z=6+23i. On a : |z|=43 et arg z=π6.
Vérifiez-le !
Une forme trigonométrique de z est z=43(cos π6+i sin π6).
3) Forme exponentielle
Exponentielle complexe
• Pour tout nombre réel θ, on pose cosθ+isinθ=eiθ.
• Les règles de calcul avec les exponentielles complexes sont les mêmes que celles avec les exponentielles réelles.
Forme (ou écriture exponentielle)
Si z =r et argz=θ, la forme trigonométrique est : z=rcosθ+isinθ. Avec la notation cosθ+isinθ=eiθ, on obtient : z=r eiθ.
Définition
L’écriture (ou forme) exponentielle du nombre complexe z de module r et d’argument θ est z=r eiθ.
Exemples
• On considère le nombre complexe z=2+2i.
On établit que z =22 et que argz=π4.
Vérifiez-le !
Une forme trigonométrique de z est z=22cosπ4+isinπ4.
Une forme (ou écriture) exponentielle de z est z=22 eiπ4.
• On considère le nombre complexe z dont la forme exponentielle est z=2 e−iπ3.
On cherche la forme algébrique de z.
z1=2cos−π3+isin−π3=212−i32=1−i3.
Utiliser les résultats du ➀B et du ➀C.
Produit de deux nombres complexes
Si z1=r1eiθ1 et z2=r1eiθ2, z1z2=r1r2eiθ1+θ2.
z1×z2=z1×z2 et argz1×z2=argz1+argz2 (à un nombre entier de tours près).
Théorème
Le module d’un produit est le produit des modules.
Un argument d’un produit est la somme des arguments (à un nombre entier de tours près).
V. Formules d’addition et de duplication
Formules d’addition des sinus et cosinus
Pour tous nombres réels a et b :
• cos (a – b) = cos a cos b + sin a sin b ;
• cos (a + b) = cos a cos b – sin a sin b ;
• sin (a + b) = sin a cos b + cos a sin b ;
• sin (a – b) = sin a cos b – cos a sin b.
Exemple
Pour tout nombre réel x, cos(2x+π4)=cos 2x cosπ4−sin 2x sinπ4 ; cosπ4=sinπ4=22. D’où : cos(2x+π4)=22cos 2x−22sin 2x.
Formules de duplication
• Pour tout nombre réel a :
sin 2a = 2 sin a cos a ;
cos 2 a = cos2 a – sin2 a.
• Pour tout nombre réel a :
cos 2a = 2 cos2 a – 1 ;
cos 2 a = 1 – 2 sin2 a.
Formules de linéarisation
Pour tout nombre réel a : cos2a=1+cos 2a2 ; sin2a=1−cos 2a2.
Exemple
Pour tout x de ℝ, cos22x=1+cos 4x2.
Utiliser une formule de duplication ou de linéarisation pour calculer une intégrale.
Exemples
• Calcul de I=∫0π4 sin2x cos2x dx
Pour tout a de ℝ, sina cosa=12 sin2a, donc sin2x cos2x=12 sin4x.
Donc I=∫0π4 12 sin4x dx,
I=12×−14cos4x0π4,
I=−18cosπ−cos0=−18−1−1.
car cosπ=−1 et cos0=1.
D’où I=−18−2=14.
Pour calculer une primitive de x↦cos4x utiliser le résultat
du ➁B du chapitre 6.
• Calcul de J=∫0π2 cos23x dx.
Pour tout a de ℝ, cos2a=1+cos2a2, donc cos23x=1+cos6x2.
Donc J=∫0π2 1+cos6x2 dx=∫0π212+12cos6x dx ;
J=12x+1216 sin6x0π2 ;
J=π4+12×16sin3π−0, puisque sin0=0 ;
sin3π=0, d’où J=π4.
Pour calculer une primitive de x↦cos6x utiliser le résultat
du ➁B du chapitre 6.
VI. Expression complexe des translations, notations et homothéties
1) Translation
Théorème 1
Soit f l’application z ↦ f(z) = z + b où b est un nombre complexe quelconque fixé.
Soit M l’image de z et soit M′ l’image de f(z) dans le plan complexe.
L’application M ↦ M’ ainsi définie est la translation de vecteur w→ où w→ est le vecteur image de b.
Exemple
On considère l’application f : z↦z+1+i.
D’après le théorème 1, f est associée à la translation de secteur w→ où w→ est le vecteur image de 1 + i.
• On a, par exemple, fi=i+1+i=1+2i.
• Si A est le point d’affixe i et B le point d’affixe 2 − i, par exemple, l’image de la droite (AB) par la translation de vecteur w→ est la droite (A′B′) où A′ est le point d’affixe fi=1+2i et B′ le point d’affixe f2−i=3.
On sait qu’une translation transforme une droite en une droite.
Faire une figure.
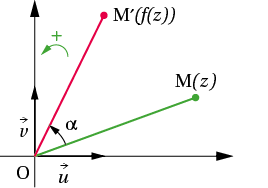
2) Rotation
Théorème 2
Soit f l’application z ↦ f(z) = a z où a = e iα est un nombre complexe fixé de module 1.
Soit M l’image de z et soit M′ l’image de f(z) dans le plan complexe orienté.
L’application M ↦ M′ ainsi définie est la rotation de centre l’origine O du repère et d’angle α.
Exemple
On considère l’application f : z↦eiπ3z.
D’après le théorème 2, f est associée à la rotation de centre l’origine O du repère et d’angle de mesure π3.
• Si A est le point d’affixe 2, l’image du point A par la rotation est le point A′ d’affixe f2=2 eiπ3=2cosπ3+isinπ3, f2=212+i32=1+i3.
• Par exemple, l’image du cercle de centre A, de rayon 2, par cette rotation est le cercle de centre A′, de rayon 2.
On sait qu’une translation transforme un cercle en un cercle de même rayon.
Faire une figure.
3) Homothétie
Théorème 3
Soit f l’application z ↦ f(z) = a z où a est un nombre réel fixé non nul.
Soit M l’image de z et soit M′ l’image de f(z) dans le plan complexe orienté.
L’application M ↦ M′ ainsi définie est l’homothétie de centre l’origine O du repère et de rapport a.
Exemple
On considère l’application f : z↦2z.
D’après le théorème 3, f est associée à l’homothétie de centre O l’origine du repère et de rapport 2.
• Si A est le point d’affixe 2i, l’image du point A par l’homothétie est le point A′ d’affixe f2i=4i. L’image du point B d’affixe 1 + i est le point B′ d’affixe f1+i=2+2i.
• L’image de la droite (AB) par cette homothétie est la droite (A′B′)
On sait qu’une homothétie transforme une droite en une droite.
Faire une figure.