L'identification d'un mouvement
A) Le système et le référentiel
En mécanique, pour étudier le mouvement d’un corps, il est nécessaire de préciser par rapport à quoi on raisonne.
On se fixe donc un référentiel d’étude. Cela consiste à étudier le mouvement des corps par rapport à un objet de référence (un solide, dans la pratique) que l’on considère immobile.
À savoir
Un système peut être soit au repos, soit en mouvement suivant le référentiel choisi.
Exemples
Un radar routier mesure la vitesse des voitures par rapport à la route. Le véhicule vert A est « flashé » à 145 km/h et la voiture bleue B à 160 km/h. Cependant, le conducteur du véhicule A voit l’autre voiture le doubler à 15 km/h seulement.
Dans un train roulant à 300 km/h, pour un passager A assis, une personne se déplace vers l’avant du train en marchant à 2 km/h. Pour un observateur sur le quai d’une gare, cette personne se déplace à 302 km/h.
B) La trajectoire
La trajectoire est la ligne formée par l’ensemble des positions prises par un point au cours de son mouvement. Elle dépend du référentiel choisi.
Une trajectoire peut être une droite, un cercle, une courbe.
Exemple
Un cycliste en mouvement lâche une balle.
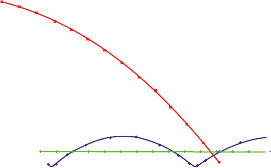
En prenant comme référentiel un point fixe extérieur, on observe la trajectoire de 3 points : la balle (en rouge), l’axe de la roue avant (en vert) et le réflecteur de cette même roue (en bleu). On schématise leurs trajectoires ci-dessous :
On constate que la trajectoire de l’axe de la roue avant est une droite, tandis que celles de la balle et du réflecteur sont des courbes.
Si on change de référentiel, en prenant par exemple l’axe de la roue (en vert), on obtient le schéma ci-contre, pour la trajectoire du réflecteur (en bleu) :
On constate à présent que cette trajectoire correspond à un cercle.
C) Le mouvement
Si la trajectoire est une droite, le mouvement est rectiligne.
Si la trajectoire est un cercle, le mouvement est circulaire.
Si la trajectoire est quelconque (c’est-à-dire qu’elle ne forme ni un cercle, ni une droite), le mouvement est curviligne.
La nature du mouvement
A) Le mouvement rectiligne
a) La vitesse moyenne
La formule de calcul de la vitesse moyenne est :
Méthode
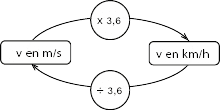
Pour convertir les kilomètres par heure en mètre par seconde et inversement, on applique le coefficient suivant :
Exemples
Le record du monde du 100 m est détenu par Usain Bolt, qui l’a couru le 16 août 2009 en 9 s 58. Sa vitesse moyenne est donc de v = ≈ 10,438 m/s, soit 10,438 × 3,6 ≈ 37,58 km/h.
Le 16 septembre 2018, le marathonien kényan Eliud Kipchoge a établi le record mondial lors du marathon de Berlin (42,195 km), avec un temps de 2 h 1 min 39 s soit une vitesse v = = 20,81 km/h.
b) La nature du mouvement
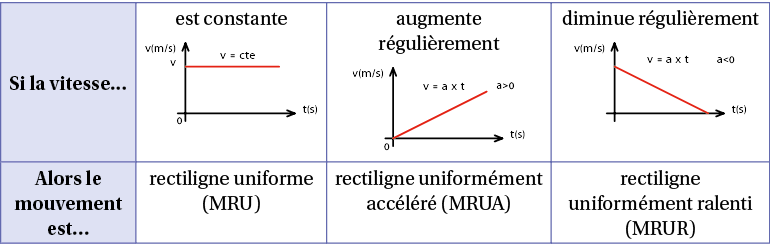
B) Le mouvement circulaire
La période de rotation, notée T, est le temps mis par un objet en mouvement circulaire pour faire un tour. Son unité est la seconde (s).
La fréquence de rotation, notée n, est le nombre de tours effectués par l’objet en une seconde. Son unité est le tour par seconde (tr/s).
À savoir
La relation qui unit n et T est :
n = .
En un tour, un point du solide parcourt une distance d égale à la circonférence c du cercle de diamètre D.
Un point d’un solide en rotation possède une vitesse linéaire, qui correspond à la distance parcourue par unité de temps, et une vitesse angulaire (ou de rotation), qui est le rapport d’un angle par unité de temps. La formule de calcul de la vitesse linéaire est :
Rappel
Calcul de la circonférence d’un cercle :
c = π × D = 2 πR
Exemple
Le remplacement des pneus d’une voiture a une incidence sur son comportement. Alors que le compteur affiche 111 km/h et son compte-tours 1 000 tr/min, la voiture est flashée à 128 km/h. On cherche à savoir à quoi est due cette différence de vitesse.
Diamètre des anciens pneus : D = 591 mm = 0,591 m.
Diamètre des nouveaux pneus : D = 678 mm = 0,678 m.
Le compte-tours indique 1 000 tr/min, soit tr/s.
La vitesse avec les anciens pneus est pour de :
v = π × D × n = π × 0,591 × .
v ≈ 30,9 m/s, soit 111 km/h.
La vitesse avec les nouveaux pneus est de :
v = π × D × n = π × 0,678 × .
v ≈ 35,5 m/s, soit 128 km/h.
Les forces
A) L’action mécanique
Toute action mécanique sur un objet est susceptible de :
– le mettre en mouvement ;
– le déformer ;
– modifier sa trajectoire ;
–le maintenir en équilibre.
B) La modélisation
Une action mécanique est modélisée par une force.
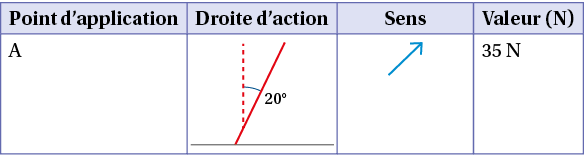
Une force est définie par 4 caractéristiques :
sa droite d’action, définie par rapport à la verticale ou à l’horizontale ;
son sens ;
sa valeur ;
son point d’application.
La valeur d’une force s’exprime en newton (N) et se mesure avec un dynamomètre.
On représente une force par un segment fléché dont la longueur est proportionnelle à la valeur de la force (définie par une échelle sur le dessin).
Exemple
C) Le poids
Le poids est la force qui modélise l’action de la Terre sur un solide. C’est une action à distance (il n’y a pas de contact) et répartie sur tout le volume de l’objet. Ses caractéristiques sont :
sa droite d’action : verticale du lieu ;
son sens : de haut en bas ;
son point d’application : le centre de gravité G du solide ;
sa valeur : en newton, mesurée à l’aide d’un dynamomètre ou calculée à l’aide de la formule suivante :

L'équilibre d'un solide
A) Soumis à l’action de deux forces
a) Définition
Un solide soumis à l’action de deux forces et est en équilibre si les deux forces ont :
la même droite d’action ;
la même valeur ;
des sens opposés.
b) Expérience
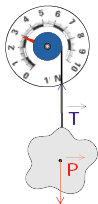
À l’aide d’un dynamomètre, on mesure le poids d’un objet quelconque.
On constate que l’objet est en équilibre sous l’action de deux forces égales et opposées : le poids et la tension du fil.
La droite d’action est commune et l’intensité du poids se lit sur le dynamomètre.
B) Soumis à l’action de trois forces
a) Définition
Un solide soumis à l’action de trois forces , et est en équilibre si :
les trois droites d’action sont coplanaires (elles sont situées dans un même plan) et concourantes (elles ont un seul point d’intersection) ;
la somme géométrique des forces est nulle, c’est-à-dire que les trois segments fléchés représentant les forces mis bout à bout forment un triangle. On dit alors que le dynamique (ou polygone) des forces est fermé.
b) Exemple
Une alpiniste descend une paroi rocheuse en rappel. Les forces s’exerçant sur l’alpiniste sont :
le poids P (en violet), appliqué au centre de gravité G ;
la tension de la corde T (en bleu), appliquée aux mains ;
la réaction du rocher R (en cyan), appliquée aux pieds.
Les trois droites sont concourantes.
La somme géométrique est nulle (dynamique fermé).

Forces s’exerçant sur l’alpiniste (à gauche) : droites d’action (au milieu) et dynamique des forces (à droite)
c) Expérience
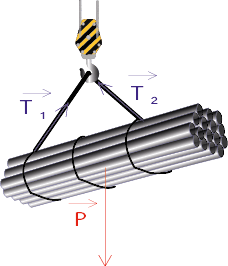
Une grue soulève une charge à l’aide de 2 élingues. On veut savoir si cette charge est en équilibre.
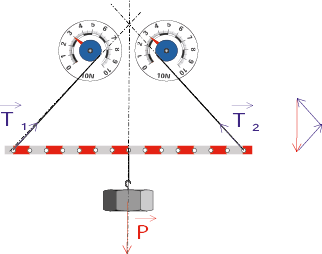
On matérialise la charge avec une barre à trous lestée en son milieu. Les forces exercées par les élingues sont caractérisées par deux dynamomètres.
La barre, soumise à 3 forces (son poids, et les deux tensions exercées par les élingues), est en équilibre. On constate dans cette expérience que les tensions sont égales. Les points d’accrochage des élingues sont à égale distance du centre de gravité G de la charge.
Définition
Une élingue est un accessoire de levage souple en cordage, en sangle, en câble métallique ou en chaîne, généralement terminé par des composants métalliques tels que maille, crochets, anneaux ou manilles.