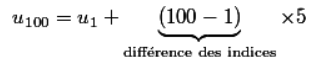Les suites arithmétiques

Nous allons étudier dans cette leçon des suites très particulières, les suites arithmétiques.

I. Exemple et définition

Exemple :

Soit la suite $-3~,~0~,~3~,~6~,~9~,~12~,\dots$.

On passe d'un terme au suivant en ajoutant la constante $3$. On dit que cette suite est arithmétique de 1^er terme $-3$ et de raison (qui est la constante que l'on ajoute systématiquement) $3$.

Définition : 

Une suite $(u)$ est une suite arithmétique s'il existe un nombre $r$ tel que pour
tout entier $n$, on a : $u_{n+1}=u_n+r$.
Le nombre $r$ est appelé raison de la suite.

Exemple : 

Soit la suite arithmétique de premier terme $u_1=8$ et de raison $5$. Donner les $5$ premiers termes de la suite. 

$u_1=8$

$u_2=8+r=8+5=13$

$u_3=u_2+r=13+5=18$

$u_4=u_3+r=18+5=23$

$u_5=u_4+r=23+5=28$

II. Forme explicite d'une suite arithmétique

Dans l'exemple précédent, on a calculé les $5$ premiers termes. Si maintenant il est demandé de calculer $u_{100}$, cela va être très fastidieux.

Entre $u_1$ et $u_2$, on ajoute $1$ fois la raison.

Entre $u_2$ et $u_3\,$, on ajoute $1$ fois la raison. Donc entre $u_1$ et $u_3\,$, on ajoute $2$ fois la raison. 

$u_3=u_1+(3-1)r$ et de proche en proche on montre que 

$u_n=u_1+(n-1)r$. 

Mais si le premier terme de la suite s'appelle $u_0$, nous avons une raison supplémentaire à ajouter et cela donne $u_n=u_0+(n-0)r$.

Afin de retenir facilement ce type de formule, on peut résumer les différentes formules en une seule : 

Revenons à l'exemple. Je connais $u_1=8$ et la raison $r=5$. On me demande $u_{100}$.

u_{100}=u_1+\underbrace{(100-1)}_{\textrm{différence des indices}}\times 5

$u_{100}=8+99\times 5=503$

III. Sens de variation d'une suite arithmétique

Soit $(u)$ une suite arithmétique de raison $r$.

Pour tout $n\in \textbf N$, $u_{n+1}=u_n+r$ ou encore en soustrayant $u_n$ aux deux membres : 

Pour tout $n\in \textbf N$, $u_{n+1}-u_n=r$

Si $\boxed{r \ge 0}$, alors $u_{n+1}-u_n \ge 0$ et $(u)$ est croissante.

Si $\boxed{r \le 0}$, alors $u_{n+1}-u_n \le 0$ et $(u)$ est décroissante.

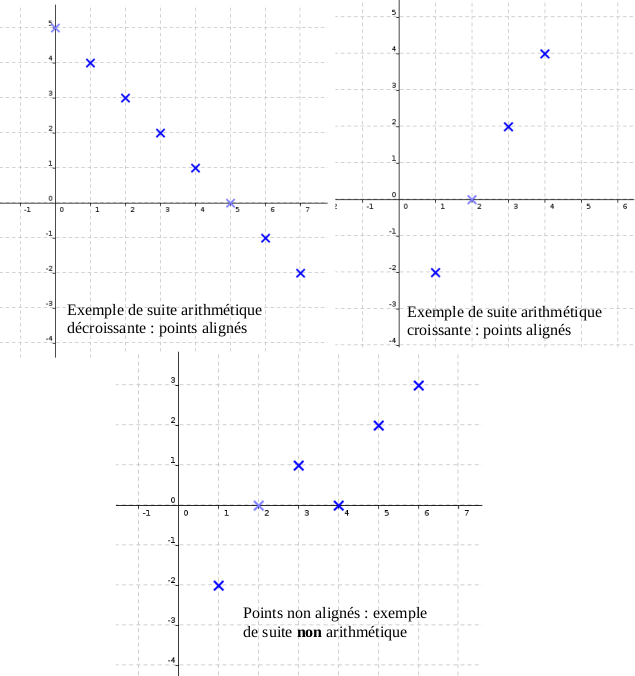
IV. Représentation graphique

Dans le cas d'une suite arithmétique, on a une variation linéaire. 

V. Exemple concret

Anne a décidé de s'acheter une petite voiture, mais ne possède qu'un capital de $9\,000$ euros alors que la voiture qu'elle convoite coûte $13425$ euros. Elle décide de garder sur son compte en banque tous les mois une somme fixe de $430$ euros, à laquelle elle ne touchera pas. Dans combien de mois Anne pourra-t-elle espérer acheter sa voiture ?

Résolution : 

Je pose $u_0=9\,000$ (exprimée en euros) la somme qu'a actuellement Anne.

Dans $1$ mois, elle aura : $u_1=u_0+430$ et de même tous les mois suivants, on aura : $u_{n+1}=u_n+430$.

La somme possédée par Anne est modélisée par une suite arithmétique de premier terme $u_0=9\,000$ et de raison $r=430$.

La somme que possédera Anne dans $n$ mois est $u_n=u_0+(n-0)r$ soit $u_n=9000+n\times 430$.

Anne veut avoir au moins $13\,4245$ euros.

Résolvons l'inéquation $u_n \ge 13\,425$

$9000+n\times 430 \ge 13\,425$

$430\times n\ge 13\,425-9000$

$430\times n\ge 4\,425$

$n\ge \dfrac{4\,425}{430}$ or $\dfrac{4\,425}{430}\approx 10,29$

Comme $n$ entier doit être supérieur à cette valeur, on peut dire que Anne aura la somme suffisante dans $11$ mois.