Les fonctions affines ont été vues en 3e puis en 2nde. Ce cours va mettre en valeur ce dont vous pouvez avoir besoin en liaison avec le programme de 1ere.
I. Définition
On appelle fonction affine, toute fonction définie sur l'ensemble des réels, noté , par où et sont deux réels.
Exemple : La fonction définie sur par est une fonction affine.
Remarque : Si le nombre on parle alors de fonction linéaire.
Ainsi la fonction définie par est linéaire. En revanche la fonction définie par n'est ni linéaire, ni affine.
Définitions : Soit est une fonction affine définie pour tous réels par .
- Le nombre est appelé coefficient directeur de la droite repésentant .
- Le nombre est appelé l'ordonnée à l'origine de la droite repésentant .
Le coefficient directeur indique « la vitesse » à laquelle la fonction progresse verticalement et l'ordonnée à l'origine est l'ordonnée du point d'intersection de la courbe représentant la fonction et l'axe des ordonnées.
Exemple : Si , le coefficient directeur est 2 et l'ordonnée à l'origine est -5.
II. Représentation graphique et variations
Propriété : La représentation graphique, dans un repère du plan, d'une fonction affine est une droite non parallèle à l'axe des ordonnées.
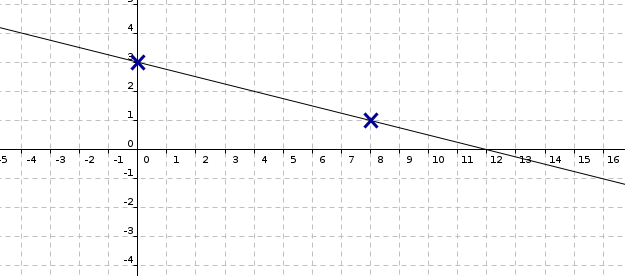
Exemple : On considère la fonction définie sur par . On souhaite en fournir une représentation graphique.
Pour cela on choisit deux nombres au hasard et on va calculer les images respectives. En théorie, ces nombres peuvent être quelconques mais dans la pratique, du fait des erreurs de tracés, il est préférable d'avoir un écart raisonnable, dépendant du repère utilisé.
Ici, on va utiliser, par exemple .
. Par conséquent la droite représentant la fonction passe par le point de coordonnées
. Par conséquent la droite représentant la fonction passe par le point de coordonnées .
Remarque : La droite représentant une fonction linéaire passe par l'origine du repère.
Variations d'une fonction affine :
Soit est une fonction affine définie sur par .
- Si > alors est croissante.
- Si < alors est décroissante.
- Si alors est constante.
III. Lien entre taux d'accroissement et coefficient directeur
Soit la fonction affine définie sur par .
Calcul du taux d'accroissement entre deux points :
Soient et (distints) les abscisses de ces deux points.
et donc
Alors :
Conclusion : le taux d'accroissement entre deux points est toujours égal au coefficient directeur de la droite représentative de la fonction affine.
Lecture graphique d'un coefficient directeur :
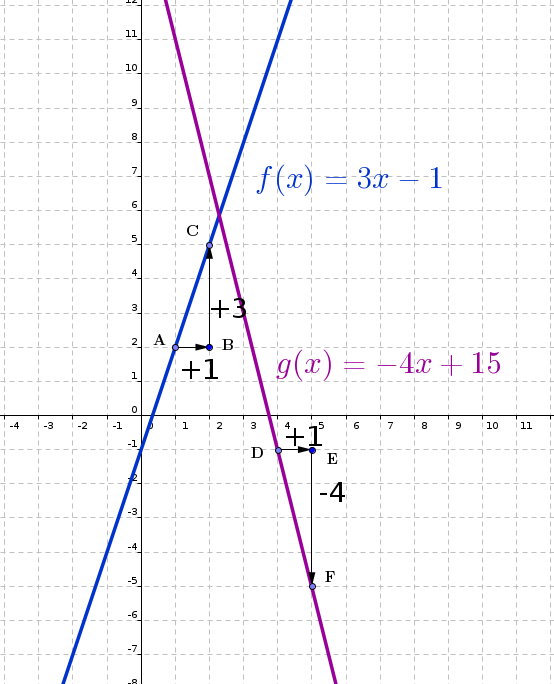
Exemple 1 : On considère la fonction affine définie sur par .
est un vecteur directeur de la droite représentant .
a pour coordonnées , dit autrement, lorsque je me décale de vers la droite, je dois « monter » de . Le coefficient directeur est .
Exemple 2 : On considère la fonction affine définie sur par .
est un vecteur directeur de la droite représentant .
a pour coordonnées , dit autrement, lorsque je me décale de vers la droite, je dois « descendre » de . Le coefficient directeur est .
Exemple 3 : On donne dans un repère du plan les points et . Donner l'expression de la fonction affine qui admet pour représentation graphique.
Résolution : Soit avec et réels.
Le nombre est égal au taux d'accroissement entre et . Donc :
Donc .
Déterminons . Je sais que la droite passe par (dit autrement lorsque je remplace par , je dois remplacer par .
soit et
En conclusion : .