La décomposition des noyaux atomiques

Légende de la leçon

Vert : définitions

I. La radioactivité

La radioactivité est la désintégration de noyaux atomiques instables. Un noyau radioactif se décompose spontanément en un noyau fils différent avec émission de particule ou de rayonnement.

1) Les quatre types d’émissions radioactives

Trois sont des émissions de particules de matière :

Le rayonnement gamma (γ) est de nature électromagnétique ; il est constitué de photons. Les rayonnements γ ont une fréquence comprise entre 3 × 10¹⁹ Hz et 3 × 10²² Hz, ce qui correspond à une longueur d’onde dans le vide λ₀ comprise entre 10⁻¹¹ et 10⁻¹⁴ m. Les rayons gamma ont des longueurs d’onde plus petites que les rayons X et donc des fréquences plus grandes : ils sont produits par désintégration radioactive, contrairement aux rayons X.

2) L’écriture d’une réaction nucléaire : les lois de conservation

Les équations de décomposition sont régies par les lois de conservation de Soddy, selon lesquelles, au cours de toute réaction nucléaire, il y a :

• conservation du nombre de charge : la somme des numéros atomiques à gauche est égale à celle à droite dans l’équation nucléaire (∑​Z1 = constante) ;
• conservation du nombre de masse ou de nucléons : la somme des nombres de masse à gauche est égale à celle à droite dans l’équation nucléaire (∑​A1 = constante).

Les équations nucléaires de décomposition sont données dans le tableau suivant :

Lors d’une réaction nucléaire α ou β, le noyau formé est initialement dans un état « excité », à cause du bouleversement important suscité par l’éjection de la particule α ou β. Le noyau retrouve son état fondamental en émettant l’excès d’énergie sous forme de radiations ou photon γ : XZA* → XZA + nγ.

Exemple

Un radio-isotope U92238 uranium 238 se décompose en N93238p neptunium 238.

L’équation nucléaire est : U92238→XZA+N93238p. Pour trouver le rayonnement émis, on utilise les lois de Soddy : 238 = A + 238 et 92 = Z + 93, ce qui permet de trouver A = 0 et Z = –1.

Le rayonnement émis est donc X−10, c’est un électron, il s’agit donc de radioactivité β^–.

II. L’évolution de la population moyenne d’un ensemble de noyaux radioactifs

1) La loi de décroissance radioactive

Le nombre de noyaux radioactifs qui se décomposent dN est proportionnel au nombre de noyaux radioactifs présents N et à la durée dt. La relation s’écrit sous forme différentielle : dN = –λ × N × dt, où λ est la constante de désintégration du noyau radioactif considéré en par seconde (s^–1) : c’est une fréquence liée à la probabilité de décomposition. dN est la variation du nombre de noyaux (ou nombre de noyaux qui se désintègrent), elle est négative.

En transformant la relation précédente, on obtient dN N = –λ × t. C’est une équation différentielle du premier ordre en N, qui ressemble à celle vue dans le cadre des réactions chimiques d’ordre 1 : d[A] [A] = –k × t[A].

En intégrant la relation, on obtient alors ln N N0 = – λ × t, où N₀ est le nombre de noyaux radioactifs présents initialement (à t = 0). On peut aussi transformer cette relation en N = N₀ × e^{-λ × t}.

2) La demi-vie radioactive t_½

On appelle demi-vie radioactive t_1/2(ou période) le temps au bout duquel l’activité est divisée par 2, c’est-à-dire où la moitié du nombre de noyaux initialement présents s’est désintégrée.

Au bout d’une demi-vie, l’activité est divisée par 2 : N = N02 ; après 2 demi-vies, l’activité est redivisée par 2, soit 4 depuis le début : N = N04 = N022.

Comme dans le cas de la cinétique d’ordre 1, la demi-vie est indépendante du nombre de noyaux de départ.

Lorsque l’on a atteint 10 demi-vies, le nombre de noyaux radioactifs de l’échantillon est considéré comme négligeable par rapport au début (il a été divisé par 2¹⁰).

Quelques exemples de radionucléides et leurs demi-vies sont donnés dans le tableau suivant. Les demi-vies radioactives sont très différentes d’un élément radioactif à un autre et même d’un isotope radioactif à un autre.

3) La relation entre la demi-vie radioactive t½ et la constante radioactive

Lorsque le temps écoulé est égal au temps de demi-réaction, alors N = N₀/2 et donc ln N N0 = – λ × t_½,soit ln 1 2 = – λ × t_½ ou Ln 2 = λ × t_½. Le temps de demi-réaction ne dépend pas de la concentration initiale en réactif. t_½ s’exprime en seconde et λ s’exprime en par seconde.

4) L’activité

L’activité A au temps t est le nombre de désintégrations par unité de temps. Elle dépend du nombre de noyaux présents et du radionucléide. L’activité est proportionnelle au nombre de noyaux radioactifs présents N : A = λ × N.

L’activité s’exprime en becquerel (Bq) : un becquerel correspond à une désintégration par seconde. L’activité d’un radioélément peut être mesurée avec un compteur Geiger-Müller.

On peut définir l’activité par unité de masse : l’unité s’exprime alors en becquerel par kilogramme (Bq.kg^–1).

Application 

Un échantillon contenant des noyaux radioactifs β^– d’iode I53131 a une activité A₀ = 1 000 Bq au temps t = 0 s. On donne l’évolution de l’activité de cet échantillon en fonction du temps sur le graphe ci-dessous.

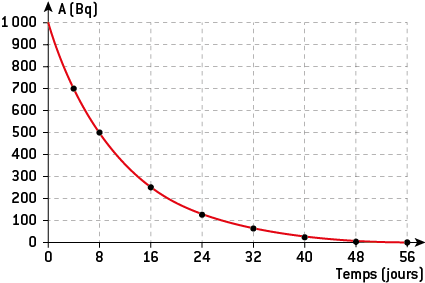
Courbe de décroissance radioactive de l’iode 131

Déterminer graphiquement la demi-vie t_1/2de l’iode 131 et en déduire sa constante radioactive λ.

Solution

Graphiquement, il faut 8 jours pour que l’activité soit divisée par 2 en passant de 1 000 à 500 becquerels : c’est la valeur de la demi-vie radioactive de l’iode 131 : t_1/2 = 8 J.

D’après la relation ln 2 = λ × t_½, on trouve la constante radioactive λ = ln 2/t_½ = 0,69/8 = 0,087 j^–1.

5) Les applications de la radioactivité

La radioactivité est employée pour les rayonnements qu’elle produit :

• en médecine : imagerie, radio, scanner, scintigraphie, radiothérapie, stérilisation des matériels et des instruments ;
• en science : datation (univers, sites) ;
• dans l’industrie : marquage ;
• en alimentation : stérilisation et conservation.

Quelques valeurs d’activités naturelles ou artificielles :

• 1 litre d’eau de pluie 0,3 à 1 Bq ;
• 1 litre d’eau de mer 10 Bq ;
• 1 litre de lait 80 Bq ;
• 1 kg de poisson 100 Bq ;
• 1 kg de pomme de terre 150 Bq ;
• 1 kg de café 1 000 Bq ;
• 1 kg de granite 1 000 Bq ;
• 1 kg d’engrais (phosphate) 5 000 Bq ;
• 1 homme (70 kg) 7 000 Bq ;
• détecteur d’incendie 30 000 Bq ;
• 1 kg de minerai d’uranium 25 MBq,
• radio-isotope pour les diagnostics médicaux 70 MBq ;
• 1 kg de déchets nucléaires de haute activité (vieux de 50 ans), vitrifiés 10 TBq ;
• 1 source radioactive médicale 100 TBq.

6) La radioprotection du personnel en présence de source radioactive

Une personne peut être exposée de deux manières :

• soit par une exposition externe : l’irradiation ;
• soit par une exposition interne : la contamination (elle peut se faire par inhalation, par ingestion de substance radioactive ou de manière cutanée).

Cette exposition a alors différents effets biologiques, qui peuvent être somatiques (sur l’organisme) ou génétiques :

• les effets somatiques apparaissent sous forme de malaises, nausées, vomissement. La peau peut aussi être brûlée. Les défenses immunitaires peuvent être réduites. Des cancers peuvent apparaître, tels que la leucémie, de manière d’autant plus probable que l’irradiation est forte ;
• au niveau génétique, une personne irradiée ou contaminée peut devenir stérile ou subir des dégâts graves : modification de l’ADN (mutations génétiques) ou des chromosomes.

La radioprotection est l’ensemble des mesures qui tendent à protéger les personnes des irradiations ou des contaminations. Il faut agir sur tous les points possibles en éloignant la source des techniciens, ainsi qu’en réduisant la dose reçue et la durée d’exposition. Le personnel travaillant dans un environnement de sources nucléaires (médecine ou centrale nucléaire) doit porter des vêtements protecteurs et se tenir à l’abri derrière des écrans sûrs (utilisation de plomb). Le travail à proximité de la source doit être limité dans le temps. De plus, un compteur de dose absorbée est accroché aux vêtements.