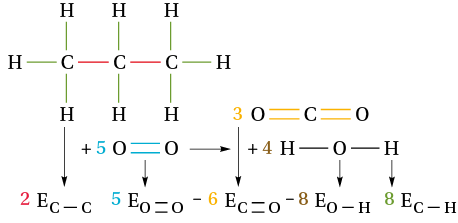L’énergie chimique

I. Le diagramme d’état d’un corps pur

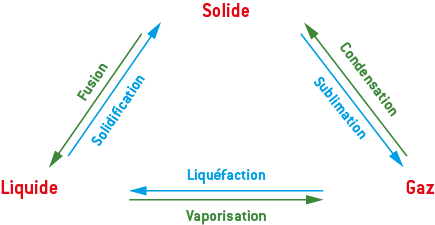
1) Les changements d’état

Le changement d’état d’un corps est une transformation physique au cours de laquelle le corps passe d’un état physique à un autre.

Un corps pur est un corps constitué d’une seule espèce chimique, contrairement à un mélange. Sous une pression donnée, le changement d’état d’un corps pur se fait à une température constante, caractéristique de ce corps pur. Cette température est appelée température de changement d’état.

Exemple

Pour l’eau, sous une pression de 1,0 bar, θ_fus = 0,0 °C et θ_vap = 100 °C.

2) Les diagrammes d’état

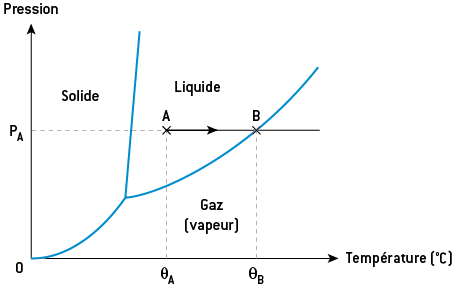
Connaissant sa température et sa pression, on peut prévoir l’état physique d’un corps pur en utilisant son diagramme d’état. Le diagramme d’état d’un corps pur est une représentation graphique en deux dimensions (pression en fonction de la température). Les trois lignes représentent les frontières entre l’état solide, l’état liquide et l’état gazeux.

3) L’enthalpie de changement d’état

Pendant un changement d’état de l’état 1 vers l’état 2, à pression constante, l’enthalpie ΔH (ou l’énergie thermique échangée) avec le milieu extérieur par une masse m d’un corps pur est égale au produit de la masse m de corps pur par l’enthalpie molaire de changement d’état Δ₁→₂H du corps pur :

Remarque

Il faut préciser le changement d’état considéré : le corps pur reçoit de l’énergie (Δ₁→₂H > 0) lors d’une fusion, d’une vaporisation ou d’une sublimation (passage vers un état moins organisé). Inversement, le corps pur cède de l’énergie (Δ₁→₂H < 0) lors d’une condensation, d’une liquéfaction ou d’une solidification (passage vers un état plus organisé).

Δ_S→_LH = –Δ_L→_SH     Δ_L→_GH = –Δ_G→_LH     Δ_S→_GH = –Δ_G→_SH

Exemple

On fait fondre une masse m = 45 g de glaçons à 0 °C. Δ_S→_LH = 334 kJ.kg^–1.

La masse vaut m = 0,045 kg, ainsi les glaçons vont recevoir une énergie ΔH = m × Δ_S→_LH = 0,045 × 334 = 15 kJ.

4) La variation d’enthalpie lors d’une variation de température

L’enthalpie d’une phase condensée varie lorsque la température passe de la température initiale T_i à la température finale T_f. Cette variation est proportionnelle à la différence de température (T_f – T_i), à la masse m de phase condensée et à la capacité thermique massique c de la phase condensée (plus c est grande, moins la variation de température est élevée pour une même masse).

Lors d’une élévation de température, la phase condensée voit son enthalpie augmenter.

Exemple

L’eau produite par la fonte des glaçons à 0 °C voit son enthalpie augmenter de 3,0 kJ. c_eau = 4,2 J.g^–1.K^–1.On peut alors calculer la température finale de l’eau. La formule ΔH = m × c_eau × (T_f – T_i), permet d’écrire (T_f - T_i) = ΔH/m × c_eau soit T_f = T_i + ΔH/m × c_eau = 0 + 3,0 × 10³/(45 × 4,2) = 16 °C.

Remarque

Lorsqu’un corps reçoit de l’énergie thermique du milieu extérieur, son enthalpie augmente, ce qui se traduit soit par une élévation de température, soit par un changement d’état, soit par une élévation de température et un changement d’état.

II. Les enthalpies standards

1) L’enthalpie standard de formation d’un corps pur ΔH_f⁰

Un corps pur simple est un corps pur ne comportant qu’un seul élément chimique : le graphite C, le dihydrogène gazeux H₂, etc. Un corps pur composé en comporte plusieurs : CO₂, H₂O, C₂H₆O, etc.

L’état standard d’un composé chimique pur est défini sous la pression standard : p° = 1 bar = 10⁵ Pa.

L’enthalpie standard de formation ΔH_f⁰(T) à la température T d’un corps pur est la différence d’enthalpie mise en jeu lors de la formation d’une mole de ce corps pur à partir des corps purs simples, considérés dans l’état standard, stables à la température considérée T. L’enthalpie standard de formation ΔH_f⁰(T) s’exprime en joule par mole (J.mol^–1).

Exemple

L’enthalpie standard de formation à T de l’eau liquide H₂O (l) est la variation d’enthalpie lors de la réaction de formation à partir du dioxygène et du dihydrogène gazeux dans l’état standard à T :

H₂ (g)+ ½ O₂ (g)→ H₂O (l).

Remarque

L’enthalpie standard de formation d’un corps simple stable, à la température T, est nulle.

2) L’enthalpie standard de réaction ∆H_r⁰ et la loi de Hess

L’enthalpie standard de réaction ΔH_r⁰ est l’énergie libérée ou prélevée au milieu extérieur par une réaction dans l’état standard.

Si la valeur de l’enthalpie standard de réaction ΔH_r⁰ est :

• positive, le système chimique reçoit de l’énergie du milieu extérieur, la réaction est endothermique ;
• négative, le système chimique cède de l’énergie au milieu extérieur, la réaction est exothermique ;
• nulle, le système chimique ne reçoit pas d’énergie du milieu extérieur ni ne lui en cède, la réaction est athermique.

L’enthalpie standard de réaction ΔH_r⁰ est déterminée à partir des enthalpies standards de formation ΔH_f⁰ des réactifs et des produits de la réaction et de leurs coefficients stœchiométriques. Si une réaction chimique s’écrit a A + b B → c C + d D, alors : ΔH_r⁰ = (d ΔH_f⁰(D) + c ΔH_f⁰(C)) – (a ΔH_f⁰(A) + b ΔH_f⁰(B)) : c’est la loi de Hess

Remarque

L’enthalpie standard ΔH_f⁰ de formation d’un corps pur est l’enthalpie standard de réaction à partir des corps simples stables dans l’état standard.

Exemple

L’équation de combustion du propane est : C₃H₈ (g) + 5 O₂ (g) → 3 CO₂ (g) + 4 H₂O (g).

ΔH_f⁰(CO₂ (g)) = –394 kJ.mol^–1, ΔH_f⁰(H₂O(g)) = – 242 kJ.mol^–1, ΔH_f⁰(C₃H₈ (g)) = 104 kJ.mol^–1 et ΔH_f⁰(O₂ (g)) = 0 kJ.mol^–1.

ΔH_r⁰ = (3 ΔH_f⁰(CO₂ (g)) + 4 ΔH_f⁰(H₂O(g))) – (ΔH_f⁰(C₃H₈ (g)) + 5 ΔH_f⁰(O₂ (g)))

= (3 × (–394) + 4 × (–242)) – (–104 + 5 × 0) = –2,05 × 10⁶ J.mol^–1 = 2,05 MJ/mol.

3) L’énergie de liaison

En phase gazeuse, la dissociation d’une liaison chimique AB conduit aux atomes A et B isolés :

AB (g) → A (g) + B (g).

Cette dissociation nécessite de l’énergie : c’est l’énergie de liaison, notée E_A-B ou E_m,A-B, exprimée en joule par mole (J.mol^–1).

Les valeurs des énergies de liaisons que l’on trouve dans les tables sont des moyennes car la force d’une liaison dépend aussi des autres liaisons établies par les atomes liés.

L’enthalpie standard de combustion ΔH_r⁰est négative puisque les combustions sont exothermiques. Elle peut être calculée de manière assez précise à partir des liaisons rompues et formées au cours de la combustion : c’est la somme des énergies des liaisons rompues moins la somme des énergies des liaisons formées : ΔH_r⁰ = Σ E_{liaisons rompues} – Σ E_{liaisons formées}.

III. L’énergie produite par une combustion

1) Le pouvoir calorifique d’un combustible

Le pouvoir calorifique massique d’un combustible, noté PC, est l’énergie dégagée par la combustion complète d’un kilogramme de combustible. Il s’exprime en joule par kilogramme (J.kg^–1).

On parle de pouvoir calorifique supérieur (PCS) si l’eau produite par la combustion est à l’état liquide. Dans le cas où l’eau formée est à l’état de vapeur, il s’agit du pouvoir calorifique inférieur (PCI).

2) Enthalpie de réaction d’une combustion

L’enthalpie de réaction d’une combustion ΔH_r mettant en jeu une masse m de combustible est calculée à partir du pouvoir calorifique massique du combustible mis en jeu : la valeur de E_lib est positive car PC est toujours positif par convention.

3) Détermination du pouvoir calorifique d’un combustible

Il faut peser un brûleur à alcool rempli d’alcool (m₀ = 160 g) et l’utiliser pour faire chauffer un bécher contenant de l’eau, le total ayant une masse m = 300 g.

On relève aussi la température de l’eau avant chauffage : θ_i, puis on fait chauffer l’eau jusqu’à obtenir une augmentation de température de l’eau de 30 °C. θ_f = θ_i + 30.

On arrête le chauffage et on pèse alors le brûleur : m₁ = 157 g. La masse m_alcool d’alcool qui a brûlé est donc m_alcool = m₁ – m₀ = 3,0 g.

La réaction subie par l’éthanol est une combustion, c’est une réaction exothermique.

L’équation de la réaction de l’éthanol avec le dioxygène de l’air est :

C₂H₆O + 3 O₂ → 2 CO₂ + 3 H₂O.

L’énergie produite par cette réaction a pu chauffer l’eau et le bécher.

On appelle ΔH_r l’enthalpie de combustion de l’alcool : c’est l’opposé de ΔH_{eau + bécher} l’enthalpie reçue par l’eau et le bécher sous forme thermique. E_lib = –Q_{eau + bécher}.

Sachant que la capacité thermique massique de l’eau est c_eau = 4,2 J.g^–1.°C^–1, la valeur de ΔH_{eau + bécher} = m.c_eau.(θ_f – θ_i) = 300 × 4,2 × 30 = 3,8 × 10⁴ J.

Cette énergie provient de la combustion, l’enthalpie de combustion de l’alcool est donc ΔH_r = –3,8 × 10⁴ J.

En supposant que l’alcool est exclusivement constitué d’éthanol, on détermine la valeur de l’enthalpie massique de combustion par gramme d’éthanol lors de sa combustion en divisant la valeur précédente par la masse d’éthanol qui a brûlé : ΔH_r/m_alcool = – 1,3 × 10⁴ J.g^–1.

Le pouvoir calorifique massique PC est la valeur absolue de l’enthalpie massique d’un kilogramme de combustible (le pouvoir calorifique est positif), soit 1 000 fois plus que la valeur précédente, soit PC_éthanol = 1,3 × 10⁷ J.kg^–1 = 13 MJ.kg^–1. On trouve environ la moitié de la valeur théorique. Ce résultat est bon malgré tout, car il y a beaucoup de pertes thermiques au cours de la manipulation.