Introduction à l’algorithme des k plus proches voisins

L’algorithme des k plus proches voisins est l’un des algorithmes utilisés dans le domaine de l’intelligence artificielle. Il intervient dans de nombreux domaines de l’apprentissage automatique.

I. Un problème de classification

Voici un problème qui peut être résolu en utilisant l’algorithme des k plus proches voisins.

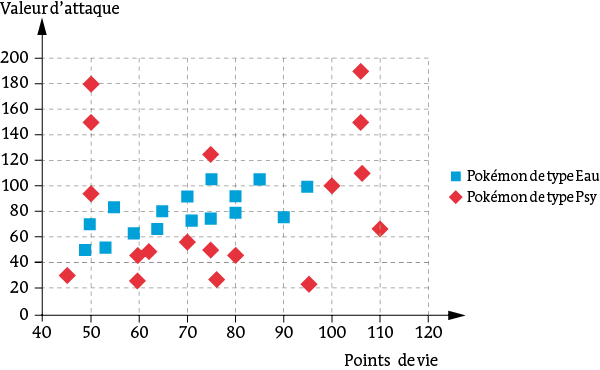
De façon très simpliste, admettons que les Pokémons ne possèdent que deux caractéristiques : leurs points de vie et leur valeur d’attaque. On suppose qu’ils se répartissent en deux types seulement : Eau et Psy.

À télécharger

Le fichier de l’échantillon pokemons.csv est disponible sur le site des éditions Hatier : hatier-clic.fr/19nsi01

À partir de cet échantillon, on veut pouvoir prédire la classification d’un Pokémon mystère à partir de la donnée de ses points de vie et de sa valeur d’attaque.

Classification d’un échantillon de 34 Pokémons

II. Algorithme de prédiction

1) À l’aide d’un diagramme

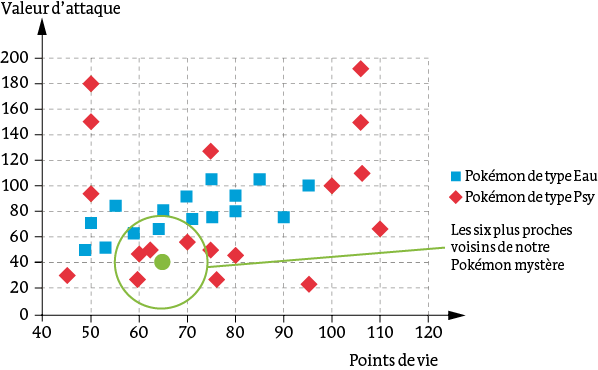
À partir des données représentées sur le diagramme, on veut prédire la classe d’un Pokémon qui a 65 points de vie et 40 en attaque. On trouve dans l’échantillon les 6 plus proches voisins :

Voisins les plus proches du Pokémon mystère

Parmi ces 6 voisins, il y a deux Pokémons de type Eau et quatre de type Psy. Il est donc probable que notre Pokémon mystère soit un Pokémon de type Psy.

2) Formulation de l’algorithme de prédiction

Pour automatiser la classification, il faut formuler un algorithme de façon formelle. Pour prédire la classe d’un Pokémon donné, il faut des données :

• un échantillon de Pokémons ;
• un Pokémon_mystère dont on veut prédire la classification ;
• la valeur de k.

Une fois ces données modélisées, la formulation de l’algorithme de prédiction est assez simple.

Algorithme :

1. Trouver, dans l’échantillon, les k plus proches voisins de Pokémon_mystère.

2. Parmi ces proches_voisins, trouver la classification majoritaire.

3. Renvoyer la classification_majoritaire.

Remarque : La valeur k = 6 est ici un choix arbitraire. Cette valeur doit néanmoins être choisie judicieusement : trop faible, la qualité de la prédiction diminue ; trop grande, la qualité de la prédiction diminue aussi. Par exemple, dans l’exemple précédent avec k = 34, la prédiction sera toujours Psy (classe majoritaire dans l’échantillon).