Exemples de forces

Parmi les forces les plus fréquentes rencontrées à l’étude des systèmes figurent le poids et la force exercée par un support ou par un fil. Elles ont chacune des caractéristiques propres.

I Poids

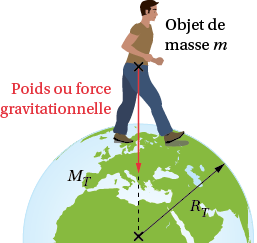Au voisinage de la Terre, tout objet de masse $m$ est soumis à une action mécanique modélisée par une force appelée poids et notée $\overrightarrow{P}$.

Ce poids s’applique au centre de gravité de l’objet, suivant la verticale et vers le bas. Sa valeur, notée P, est proportionnelle à la masse de l’objet :

Le poids $\overrightarrow{P}$ d’un objet résulte de l’attraction de la Terre. Il peut être assimilé à la force gravitationnelle ${\overrightarrow{F}}_{\text{T/O}}$ exercée par la Terre sur cet objet.

Si $\overrightarrow{P}={\overrightarrow{F}}_{\text{T/O}}=-G\times \frac{M_{\text{T}}\times m}{d^2} \overrightarrow{u}$, alors $mg=\text{G}\times \frac{m\times M_{\text{T}}}{d^2}$ et $g=\text{G}\times \frac{M_{\text{T}}}{d^2}$.

Sur Terre : $d=R_{\text{T}}=6380\text{km}=\mathrm{6,38}\times {10}^6\text{m}$ et MT = 5,98 × 10²⁴ kg.

D’où $g=\mathrm{6,67}\times {10}^{-11}\times \frac{\mathrm{5,98}\times {10}^{24}}{{(\mathrm{6,38}\times {10}^6)}^2}=\mathrm{9,80}\text{ N}\cdot {\text{kg}}^{-\text{1}}$.

II Force exercée par un support ou par un fil

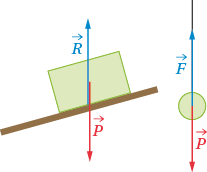
Lorsqu’un objet est immobile, posé sur un support ou suspendu par un fil, il exerce sur le support ou le fil une force verticale et vers le bas, liée à son poids $\overrightarrow{P}$. D’après le principe des actions réciproques, le support exerce sur l’objet une force opposée $\overrightarrow{R}$ et le fil exerce une force opposée $\overrightarrow{F}$.

Dans ce cas, les forces exercées sont souvent verticales et vers le haut.

Repère
À noter

Les forces décrites ci-dessus peuvent être déterminées en utilisant le principe d’inertie.

MéthodeCalculer le poids en différents endroits

a. Déterminer la valeur du poids d’un astronaute A, de 75,3 kg, lorsqu’il se trouve à Paris puis à l’équateur.

b. Quelle est l’intensité de la force gravitationnelle exercée sur lui par la Terre dans une station spatiale à 400 km d’altitude ?

c. En assimilant l’attraction gravitationnelle avec le poids, déterminer la valeur de la pesanteur g dans la station. L’intensité de pesanteur dépend-elle de l’altitude ?

d. Le même astronaute se trouve sur la Lune. Comparer son poids sur la Lune à celui sur la Terre. Expliquer la différence observée.

Données :

• gParis = 9,81 N · kg^–1 ; géquateur = 9,79 N · kg^–1 ; gLune = 1,62 N · kg^–1 ;

• masse de la Terre : MT = 5,98 × 10²⁴ kg ;

• rayon de la Terre : $R_{\text{T}}=6380\text{ km}$.

Repère
Conseils

a. Utilisez l’expression mathématique reliant le poids d’un objet à sa masse.

b. Utilisez l’expression de la force d’interaction gravitationnelle.

c. Utilisez la relation FT/A = P = mg en faisant attention aux unités.

d. Calculez le quotient $\frac{P_{\text{Terre}}}{P_{\text{Lune}}}$ et comparez les masses des astres.

Solution

a. $P_{\text{Paris}}=m\times g_{\text{Paris}}=\mathrm{75,3}\times \mathrm{9,81}=739\text{ N}$.

$P_{\text{équateur}}=m\times g_{\text{équateur}}=\mathrm{75,3}\times \mathrm{9,79}=737\text{N}$.

b. À 400 km d’altitude, la distance au centre de la Terre est :

6 380 + 400 = 6 780 km.

$F_{\text{T/A}}=\text{G}\times \frac{m\times M_{\text{T}}}{d^2}=\mathrm{6,67}\times {10}^{-11 }\times \frac{\mathrm{5,98}\times {10}^{24}\times \mathrm{75,3}}{{\left(\mathrm{6,78}\times {10}^{6 }\right)}^2}=653\text{N}$.

c. Soit gS l’intensité de pesanteur dans la station.

FT/A = P = m × g, donc $g_S=\frac{F_{\text{T/A }}}{m}=\frac{653}{\mathrm{75,3}}=\mathrm{8,67}\text{N}\cdot {\text{kg}}^{-\text{1}}$.

La valeur de la pesanteur diminue lorsque l’altitude augmente

d. Poids de l’astronaute sur la Lune : $P_{\text{Lune}}=m\times g_{\text{Lune}}=\mathrm{75,3}\times \mathrm{1,62}=122\text{ N}$.

Ainsi $\frac{P_{\text{Terre}}}{P_{\text{Lune}}}=\frac{739}{122}$ = 6,06 ≈ 6. Le poids sur la Terre est donc environ 6 fois plus grand que sur la Lune. Ceci est dû à la différence de masse : la Lune moins massive attire moins les objets que la Terre.