Le phénomène de dispersion par un prisme s’explique par les deux réfractions subies par la lumière lorsqu’elle traverse le prisme et par la variation de l’indice optique du milieu en fonction de la longueur d’onde.
I. Décomposition de la lumière blanche par un prisme
Lorsqu’un fin faisceau de lumière blanche traverse un prisme de verre, on observe un spectre continu formé d’une multitude de lumières colorées juxtaposées, appelées radiations monochromatiques.
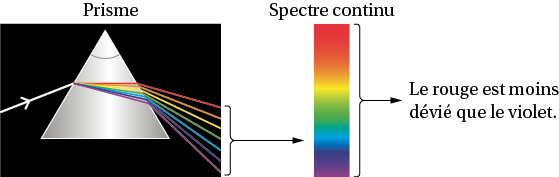 II. Interprétation de la dispersion de la lumière blanche
II. Interprétation de la dispersion de la lumière blanche
Dans un milieu dispersif (verre, eau, …), l’indice optique dépend de la couleur et donc de la longueur d’onde de la lumière monochromatique qui le traverse.
Exemple :
Un arc-en-ciel est le résultat de la décomposition de la lumière solaire par les gouttes de pluie. C’est la preuve que l’eau est un milieu dispersif.
Pour un même angle d’incidence dans l’air (d’indice ), l’angle de réfraction dans le verre est tel que :
(d’après la 2e loi de Snell-Descartes pour la réfraction).
L’indice du verre dépend de la couleur de la lumière monochromatique qui le traverse, donc l’angle en dépend également.
Ce phénomène de dispersion permet de décomposer la lumière blanche en séparant les radiations monochromatiques qui la constituent.
Repère
À noterLe rouge est moins dévié que le violet car l’indice optique du rouge est plus faible que celui du violet.

Méthode - Interpréter la dispersion de la lumière par un prismeLa courbe suivante représente les variations de l’indice optique du verre d’un prisme en fonction de la longueur d’onde de la lumière dans le vide.a. Montrer que la 2e loi de Snell-Descartes pour la première réfraction subie par la lumière à l’entrée dans le prisme peut s’écrire : .b. Pour un rayon de lumière blanche arrivant sur le prisme avec un angle d’incidence de 45°, calculer la valeur de l’angle de réfraction pour chacune des limites du visible.c. Expliquer pourquoi on dit que le rouge est moins dévié que le violet.
Repère
Conseilsa. Exprimez la 2e loi de Snell-Descartes pour la réfraction en réfléchissant aux valeurs des indices optiques de chacun des deux milieux.b. Utilisez la touche sin−1 (ou Asn) de la calculatrice.c. Définissez la déviation du rayon lumineux par un angle.
Solution

