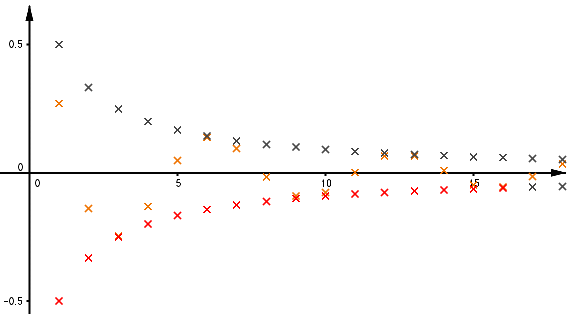👉 Des fiches d'exercices (non visibles actuellement sur l'application) existent, elles sont disponibles depuis le site internet https://www.digischool.fr/lycee
Voici des démonstrations du cours sur les suites numériques.
Démonstration 1 : le théorème de comparaison
Théorème de comparaison
On considère deux suites (un) et (vn) telles qu'à partir d'un certain rang on ait un⩽vn.
1. Si n→+∞limun=+∞ alors n→+∞limvn=+∞.
2. Si n→+∞limvn=−∞ alors n→+∞limun=−∞.
On ne va montrer que le premier point, le second fonctionnant de la même façon.
On appelle n1 le rang à partir du quel on a un⩽vn. Soit A un réel.
Puisque n→+∞limun=+∞, il existe un rang n2 tel que, pour tout entier naturel n⩾n2, un∈[A;+∞[.
On appelle n0 le maximum de n1 et n2. Ainsi pour tout entier naturel n⩾n0 on a vn⩾un⩾A.
Par conséquent n→+∞limvn=+∞.
Démonstration 2 : le théorème des gendarmes
Théorème des gendarmes
On considère trois suites (un), (vn) et (wn) et un nombre réel ℓ. On suppose qu'il existe un rang à partir duquel vn⩽un⩽wn et que n→+∞limvn=n→+∞limwn=ℓ. Alors n→+∞limun=ℓ.
Soit I un intervalle ouvert contenant ℓ.
On appelle n1 le rang à partir duquel vn⩽un⩽wn
La suite (vn) converge vers ℓ.
On appelle n2 le rang à partir duquel tous les termes de la suite appartiennent à I.
La suite (wn) converge vers ℓ.
On appelle n3 le rang à partir duquel tous les termes de la suite appartiennent à I.
On appelle n0 le plus grand des trois entiers n1,n2 et n3.
Par conséquent, pour tout entier naturel n⩾n0, l'intervalle I contient tous les termes vn et wn.
De plus on a vn⩽un⩽wn.
Par conséquent un∈I. Donc n→+∞limun=ℓ.
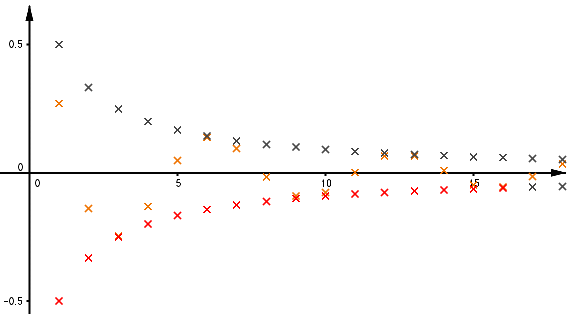
Les termes de la suite (un) compris entre ceux des deux suites (vn) et (wn) tendent vers la même limite.
Démonstration 3 : les suites monotones
Propriété :
1. Si une suite (un) croissante converge vers un réel ℓ alors pour tout entier naturel n on a un⩽ℓ.
2. Si une suite (un) décroissante converge vers un réel ℓ alors pour tout entier naturel n on a un⩾ℓ.
On démontre le premier point par l'absurde ; le deuxième fonctionnant de la même façon.
On suppose qu'il existe un rang n0 tel que un0⩾ℓ.
La suite (un) est croissante, par conséquent pour tout entier naturel n⩾n0 on a un⩾ℓ.
L'intervalle ]ℓ−1;un0[ contient ℓ mais aucun des termes un à partir du rang n0.
Cela contredit le fait que la suite converge vers ℓ.
L'hypothèse faite est donc fausse et, pour tout entier naturel n on a un⩽ℓ.
(voir démonstration 3 du fichier dédié).
Démonstration 4 : les suites croissantes majorées ou décroissantes minorées
Propriété : Une suite croissante non majorée a pour limite +∞.
On considère un réel A et une suite (un) croissante non majorée.
Il existe donc un rang n0 tel que un0>A.
La suite étant croissante on a donc, pour tout entier naturel n>n0, un⩾un0>A. Tous les termes de la suite appartiennent donc à l'intervalle [A;+∞[ à partir du rang n0. Par conséquent n→+∞limun=+∞.
Démonstration 5 : la propriété qui va permettre de conclure pour les suites géométriques
On veut démontrer que :
Si a est un réel strictement positif, alors pour tout entier naturel n on a :
(1+a)n⩾1+na.
Nous allons utiliser un raisonnement par récurrence.
Initialisation : Prenons n=0. Alors (1+a)0=1. et 1+0×a=1. Par conséquent, on a bien (1+a)0⩾1+0×a La propriété est donc vraie au rang 0.
Hérédité : Supposons la propriété vraie au rangp: (1+a)p⩾1+pa Alors : (1+a)p+1=(1+a)×(1+a)p
(1+a)p+1⩾(1+a)×(1+pa)
(1+a)p+1⩾1+pa+a+pa2
(1+a)p+1⩾1+(p+1)a+pa2
(1+a)p+1⩾1+(p+1)a car pa2⩾0
La propriété est donc vraie au rang p+1.
Conclusion : La propriété est vraie au rang 0 et est héréditaire. Par conséquent, pour tout entier naturel n, on a : (1+a)n⩾1+na
Démonstration 6 : un résultat pour les suites géométriques
Propriété : On considère une suite géométrique (un) de premier terme u0 et de raison q.
Si q⩽−1 alors la suite (un) n'a pas de limite.
Si −1<q<1 alors n→+∞limun=0.
Si q=1 alors n→+∞limun=u0.
Si q>1 alors n→+∞limun=+∞si u0>0
Si q>1 alors n→+∞limun=−∞si u0<0
On ne montrera que le dernier point.
Puisque q>1 cela signifie qu'il existe un réel strictement positif a tel que q=1+a.
La suite (un) est géométrique.
Par conséquent, pour tout entier naturel n on a : un=u0qn=u0(1+a)n
D'après la propriété précédente, on a (1+a)n⩾1+na Or n→+∞lim1+na=+∞.
D'après le théorème de comparaison, n→+∞lim(1+a)n=+∞
∘ Si u0>0 alors n→+∞limun=+∞
∘ Si u0<0 alors n→+∞limun=−∞
Merci à Eh01 et Malou pour avoir participé à l'élaboration de cette contribution