Critère de colinéarité

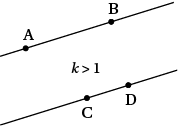
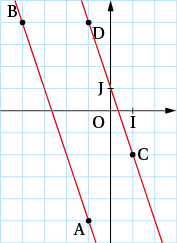
La notion de vecteurs colinéaires permet de traduire en langage vectoriel la notion de parallélisme. On découvre à travers cette transposition de nouvelles façons d’utiliser les propriétés des droites parallèles.

I Colinéarité

1 Définition

Soit 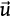et $\overrightarrow{v}$ deux vecteurs non nuls.

Dire que $\overrightarrow{u}$ est colinéaire à $\overrightarrow{v}$ signifie qu’il existe un réel k vérifiant l’égalité :

$\overrightarrow{v}=k\overrightarrow{u}$

On en déduit que si $\overrightarrow{u}$ est colinéaire à $\overrightarrow{v}$, alors $\overrightarrow{v}$ est colinéaire à $\overrightarrow{u}$ puisque l’on peut écrire $\overrightarrow{u}=\frac{1}{k}\overrightarrow{v}$. On dit aussi que les vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$ sont colinéaires.

Par extension, on dit que le vecteur nul est colinéaire à tous les vecteurs du plan.

2 Conséquences

Dire que les vecteurs $\overrightarrow{\text{AB}}$ et $\overrightarrow{\text{CD}}$ sont colinéaires signifie que les droites (AB) et (CD) sont parallèles.

En effet, s’il existe un réel k tel que $\overrightarrow{\text{AB}}=k\overrightarrow{\text{CD}}$, alors $\overrightarrow{\text{AB}}$ et $\overrightarrow{\text{CD}}$ ont la même direction, ce qui signifie que (AB) et (CD) sont parallèles.

Dire que les vecteurs $\overrightarrow{\text{AB}}$ et $\overrightarrow{\text{AC}}$ sont colinéaires signifie que les points A, B et C sont alignés.

En effet, si $\overrightarrow{\text{AB}}$ et $\overrightarrow{\text{AC}}$ sont colinéaires, alors (AB) et (AC) sont parallèles. Comme ces droites ont un point en commun (le point A), elles sont confondues. Il en résulte que les points A, B, C sont alignés sur cette droite.

II Déterminant et colinéarité

Le déterminant de deux vecteurs $\overrightarrow{u}(x;y)$ et $\overrightarrow{u^{\prime }}(x^{\prime };y^{\prime })$ est le nombre :

det(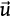 ; $\overrightarrow{v}$) = xy′ – x′y

Repère
À noter

La démonstration figure dans la méthode.

Test de colinéarité. Les deux vecteurs $\overrightarrow{u}(x;y)$ et $\overrightarrow{u^{\prime }}(x^{\prime };y^{\prime })$ sont colinéaires si et seulement si leur déterminant est nul : xy′ – x′y = 0.

Remarque : leur déterminant est donc différent de 0 si et seulement si ces deux vecteurs ne sont pas colinéaires.

Méthode

1 Démontrer le test de colinéarité utilisant le déterminant

Repère
À noter

1. Utiliser la définition de deux vecteurs colinéaires.

2. Étudier le cas où x′ = 0 et y′= 0, puis le cas contraire, soit x′ ≠ 0 ou y′ ≠ 0.

1. On suppose que les deux vecteurs $\overrightarrow{u}(x;y)$ et $\overrightarrow{u^{\prime }}(x^{\prime };y^{\prime })$ sont colinéaires. Démontrer que leur déterminant est nul.

2. Réciproquement, on suppose que xy′ – x′y = 0. Montrer que les deux vecteurs $\overrightarrow{u}(x;y)$ et $\overrightarrow{u^{\prime }}(x^{\prime };y^{\prime })$ sont colinéaires.

solution

1. Il existe un réel k tel que $\overrightarrow{u^{\prime }}=k\overrightarrow{u}$. Les coordonnées de $k\overrightarrow{u}$ étant (kx ; ky) on a x′ = kx et y′ = ky donc le déterminant vaut xy′ – x′y = kxy – kxy = 0.

2. Réciproquement, supposons que xy′ – x′y = 0.

Si x′ = y′ = 0 alors $\overrightarrow{u^{\prime }}=\overrightarrow{0}$ et le vecteur nul étant colinéaire à tout vecteur, $\overrightarrow{u}$ et $\overrightarrow{u^{\prime }}$ sont colinéaires.

Sinon l’un des deux nombres x′ ou y′ est différent de 0. Supposons par exemple que l’on ait x′ ≠ 0. Alors $x{y}^{\prime }–x^{\prime }y=0\iff x^{\prime }y=x{y}^{\prime }\iff y=\frac{x{y}^{\prime }}{x^{\prime }}$. Donc :

$\overrightarrow{u}=x\overrightarrow{i}+x\frac{y^{\prime }}{x^{\prime }}\overrightarrow{j}=x\left(\overrightarrow{i}+\frac{y^{\prime }}{x^{\prime }}\overrightarrow{j}\right)=\frac{x}{x^{\prime }}(x^{\prime }\overrightarrow{i}+y^{\prime }\overrightarrow{j})=\frac{x}{x^{\prime }}\overrightarrow{u^{\prime }}$.

Cela prouve que $\overrightarrow{u}$ et $\overrightarrow{u^{\prime }}$ sont colinéaires.

2 Utiliser la colinéarité de deux vecteurs

On considère les points A(–1 ; –5), B(–4 ; 4), C(1 ; –2) et D(–1 ; 4). Les droites (AB) et (CD) sont-elles parallèles ?

conseilS

La question revient à savoir si les vecteurs $\overrightarrow{\text{AB}}$ et $\overrightarrow{\text{CD}}$ sont colinéaires.

solution

$\overrightarrow{\text{AB}}$ = $\left(\begin{array}{c}–4–(–1)\\ 4–(–5)\end{array}\right)=\left(\begin{array}{c}\text{–}3\\ 9\end{array}\right)$ et $\overrightarrow{\text{CD}}$ = $\left(\begin{array}{c}–1–1\\ 4–(–2)\end{array}\right)=\left(\begin{array}{c}–2\\ 6\end{array}\right)$.

On calcule le déterminant : (–3) × 6 – (–2) × 9 = –18 – (–18) = 0.

Par conséquent les vecteurs $\overrightarrow{\text{AB}}$ et $\overrightarrow{\text{CD}}$ sont colinéaires et donc les droites (AB) et (CD) sont parallèles.

Remarque : Si $\overrightarrow{u}$ a pour coordonnées (-1 ; 3) alors $\overrightarrow{\text{AB}}=3\overrightarrow{u}$ et $\overrightarrow{\text{CD}}=2\overrightarrow{u}$.