Dans un plan, un point peut être positionné précisément par la donnée de ses coordonnées. De même, les vecteurs peuvent aussi être décrits par des coordonnées.
I Coordonnées dans un repère
1 Repère orthonormé du plan
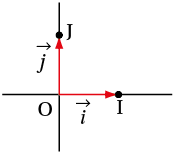
Un repère orthonormé du plan est un ensemble de trois points O, I, J tels que le triangle OIJ soit rectangle et isocèle en O. Le point O s’appelle l’origine du repère.
On peut ainsi définir les deux vecteurs, appelés vecteurs de base, et tels que et .
2 Abscisse et ordonnée d’un point, d’un vecteur
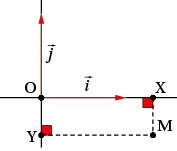
Considérons les points M, X (sur l’axe des abscisses) et Y (sur l’axe des ordonnées). Le quadrilatère OXMY est un rectangle.
Comme et sont colinéaires, il existe un nombre x tel que . On peut aussi écrire .
On a alors : .
x s’appelle l’abscisse du point M, et aussi l’abscisse du vecteur .
y s’appelle l’ordonnée du point M, et aussi l’ordonnée du vecteur
x et y s’appellent les coordonnées du point M, et aussi du vecteur
Repère
À noterDans un repère orthonormé, les coordonnées d’un point sont uniques, tout comme celles d’un vecteur.
On considère deux points A et B de coordonnées respectives (xA ; yA) et (xB ; yB). Alors le vecteur a pour coordonnées (xB – xA ; yB – yA).
Deux vecteurs sont égaux si, et seulement si, ils ont les mêmes coordonnées.
II Somme de deux vecteurs
Si et ont pour coordonnées (x ; y) et (x′ ; y′) alors :
• a pour coordonnées (x + x′ ;y + y′) donc :
• a pour coordonnées (kx ;ky) donc :
Méthode
1 Lire les coordonnées d’un vecteur graphiquement
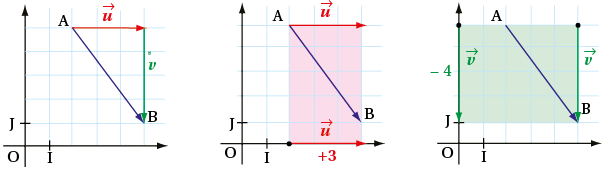
Dans un repère (O, I, J), on donne les points A(2 ; 5) et B(5 ; 1).
Lire graphiquement les coordonnées du vecteur sans utiliser de formule.
Repère
ConseilSPartant de A, on se dirige vers B en effectuant un trajet horizontal puis vertical. On peut aussi faire l’inverse : suivre un trajet vertical puis horizontal.
solutionSur la figure, on voit que avec et .
On en déduit que . Les coordonnées de sont donc (3 ; –4).
2 Déterminer les coordonnées d’un point sous contraintes.
On donne les points A(4 ; 1), B(2 ; –3) et C(–1 ; –2). Trouver les coordonnées du point D pour que ABCD soit un parallélogramme.
conseilSLes coordonnées de D sont (x ; y) et se calculent sachant que .
solutionLes coordonnées des vecteurs et sont respectivement et . Donc a pour coordonnées .
Le vecteur ayant pour coordonnées , est donc équivalent à x – 2 = –1 et y + 3 = 5. D’où x = 1 et y = 2.