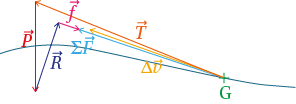Vecteurs vitesse et forces

Lorsqu’un système est soumis à des actions mécaniques, il peut être mis en mouvement ou voir son mouvement initial modifié : sa trajectoire et/ou sa vitesse peuvent changer, notamment sous l’effet des forces.

I Variation du vecteur vitesse en un point

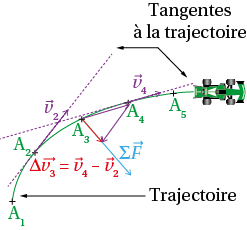
Dans toutes les études de mouvement, on assimilera le système étudié à un point matériel.

En chaque point, on peut définir le vecteur vitesse du système étudié : sa direction est tangente à la trajectoire, son sens est celui du mouvement et sa norme est égale au quotient du vecteur déplacement $\overrightarrow{{\text{A}}_{i–1}{\text{A}}_{i+1}}$ sur la durée Δt qui sépare ces deux instants : $\overrightarrow{v}=\frac{\overrightarrow{{\text{A}}_{i–1}{\text{A}}_{i+1}}}{\Delta t}$.

La variation du vecteur vitesse en un point est égale à la différence entre le vecteur vitesse du point précédent et celui du point suivant.

II Influence des forces sur un mouvement

Une force est la modélisation d’une action mécanique. Effectuer un bilan des forces consiste à identifier et nommer toutes les forces appliquées à un système.

La somme des forces appliquées à un système est égale à la somme vectorielle de toutes les forces appliquées au système : $\sum \overrightarrow{F}={\overrightarrow{F}}_1+{\overrightarrow{F}}_2+{\overrightarrow{F}}_3+\mathrm{...}$

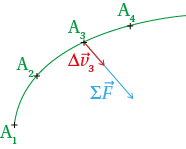
En tout point, la somme des forces appliquées à un système est colinéaire à la variation du vecteur vitesse du système : les deux vecteurs auront même direction, même sens et il existera entre leurs normes une « rela­tion approchée » de proportionnalité dont le coefficient sera noté k et sera proportionnel à la masse du système :

${\sum }^{\text{}}\overrightarrow{F} =k\times \Delta \overrightarrow{v}$

Repère
À noter

L’effet d’une force sur la variation du vecteur vitesse est d’autant plus faible que la masse est importante.

Déterminer graphiquement la somme des forces appliquées

On étudie le mouvement d’un kitesurfeur sur sa planche. Il est soumis à son poids $\overrightarrow{P}$, à la réaction de l’eau $\overrightarrow{R}$, aux frottements de l’eau $\overrightarrow{f }$ et à la traction de la voile $\overrightarrow{T}$. On modélise le sportif et sa planche par un point G.

a. Représenter la somme des forces appliquées au système au point G.

b. Déterminer la direction et le sens du vecteur variation du vecteur vitesse au point G. Justifier.

c. On connait le coefficient de proportionnalité k = 105 kg · s⁻¹ entre la somme des forces et le vecteur variation de vitesse. Sachant que la somme des forces à une norme de 2,63 × 10³ N, déterminer la norme du vecteur variation de vitesse.

d. Tracer sur un schéma les vecteurs somme des forces et variation de vitesse (échelles : 1 cm pour 1 000 N et 10 m· s⁻¹).

Repère
Conseils

a. Conservez la direction et la longueur de chaque vecteur.

b. et
c. La variation du vecteur vitesse et la somme des forces appliquées sont proportionnelles.

solution

a. et
d.

b. La somme des forces appliquées et la variation du vecteur vitesse sont colinéaires. Elles ont donc même direction et même sens.

c. D’après la relation ${\sum }^{\text{}}\overrightarrow{F}=k\times \Delta \overrightarrow{v}$, nous pouvons écrire :

${\sum }^{\text{}}F=k\times \Delta v$, d’où $\Delta v=\frac{{\sum }^{\text{}}\text{F}}{k}=\frac{\mathrm{2,63}\times {10}^3}{105}=25 \text{m}\cdot {\text{s}}^{–1}$.

d. Détermination des longueurs des vecteurs sur le schéma :

Intensité (N)	1 000	2,63 × 103		Vitesse (m·s–1)	10	25
Longueur (cm)	1,0	2,6		Longueur (cm)	1	2,5