Une prévision mathématique des fréquences alléliques

icône de pdf
Signaler
Le modèle mathématique de Hardy-Weinberg prévoit une stabilité théorique de la fréquence des allèles au sein d’une population.

I. Modèle de Hardy-Weinberg et fréquences des allèles

Hardy et Weinberg ont formulé au XXe siècle un modèle de transmission des allèles au cours d’une génération pour une population « idéale ».
Ce modèle avance une stabilité des fréquences relatives des allèles d’un gène donné au cours des générations au sein de cette population idéale. Un tableau de croisements permet de prévoir les fréquences des génotypes à la génération suivante.

Fréquence des génotypes à la génération suivante

Considérons un gène à deux allèles (AA et aa). Pour une génération donnée, si pp est la fréquence de l’allèle AA (c'est-à-dire f(A)=pf(A) = p, avec 0<p<1) 0 \lt p \lt 1) et qq (c'est-à-diref(a)=qf(a) = q, avec 0<q<10 \lt q \lt 1) la fréquence de l’allèle aa, on a p+q=1\boxed{p + q = 1}.
Cela permet d’établir le tableau de croisement suivant, considérant une répartition identique des fréquences de ces allèles AA et aa chez l'homme (p+q)(p+q) et la femme (p+q)(p+q), soit :
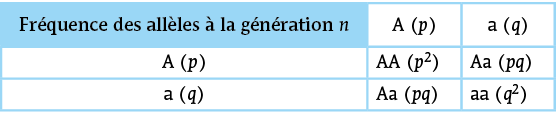255c82b2-fe61-4a18-9087-78bf44444d18Doc - Fréquence des génotypes à la génération n + 1
(Nota : éventuellement passer le téléphone en mode paysage)
Ainsi, on peut lire que la fréquence des génotype à la génération n+1n+1 vaut :
f′(AA)+f′(Aa)+f′(aa)=p2+2pq+q2=(p+q)2=1\boxed{f'(AA) + f'(Aa) + f'(aa) = p^2+2pq+q^2= (p+q)^2=1}

Fréquence des allèles à la génération suivante

Considérons une nouvelle génération de NN individus diploïdes (= cellules dont les chromosomes qu'elle contient sont présents par paires ⇒2N\Rightarrow 2N chromosomes). Le gène considéré a donc deux allèles (AA et aa).
La fréquence des génotypes dans cette nouvelle génération vaut (nota : mettre le téléphone en mode paysage si besoin) :
f′(AA)=nombre d’individus ayant le geˊnotype AAN=n(AA)Nf'(AA) = \dfrac{\text{nombre d'individus ayant le génotype AA}}{N}=\dfrac{n(AA)}{N};
f′(Aa)=nombre d’individus ayant le geˊnotype AaN=n(Aa)Nf'(Aa) = \dfrac{\text{nombre d'individus ayant le génotype Aa}}{N}=\dfrac{n(Aa)}{N};
f′(aa)=nombre d’individus ayant le geˊnotype aaN=n(aa)Nf'(aa) = \dfrac{\text{nombre d'individus ayant le génotype aa}}{N}=\dfrac{n(aa)}{N}.
La fréquence des allèles AA exprimés dans le génotype de cette nouvelle génération vaut alors (nota : mettre le téléphone en mode paysage si besoin) :
  • f′(A)=nombre d’alleˋles A exprimeˊs dans le geˊnotype de ces individus2Nf'(A)=\dfrac{\text{nombre d'allèles A exprimés dans le génotype de ces individus}}{2N}


    ⇔f′(A)=2×n(AA)+n(Aa)2N\Leftrightarrow f'(A)=\dfrac{2 \times n(AA) + n(Aa)}{2N} (il y a bien 2 allèles A dans l'individu de génotype AA)

    ⇔f′(A)=2×f′(AA)+f′(Aa)2\Leftrightarrow \boxed{f'(A)=\dfrac{2 \times f'(AA) + f'(Aa)}{2}}
  • Par ce même raisonnement, on en déduit que :
    f′(a)=2×f′(aa)+f′(Aa)2\boxed{f'(a)=\dfrac{2 \times f'(aa) + f'(Aa)}{2}}

Démonstration de la stabilité des fréquences des allèles

Soit f(A)f(A) la fréquence de l’allèle AA à la génération nn, f′(A)f'(A) sa fréquence à la génération n + 1. On a vu que :
f ′(A)=2f′(AA)+f′(Aa)2f '(A) = \dfrac{2f'(AA) + f'(Aa)}{2}
⇔f ′(A)=p2+12×2pq\Leftrightarrow f '(A)=p^2 + \dfrac{1}{2} \times 2pq en lisant le Doc "fréquence des génotypes à la génération n+1n+1"

⇔f′(A)=p2+pq\Leftrightarrow f'(A)= p^2 + pq par simplification
⇔f′(A)=p(p+q)\Leftrightarrow f'(A)= p (p + q) par factorisation
⇔f′(A)=p=f(A)\Leftrightarrow f'(A) = p = f(A) sachant que p+q=1p+q=1
Ainsi, la fréquence de l’allèle AA à la génération n+1n + 1 est bien la même qu’à la génération nn.

II. Conditions pour valider le modèle de Hardy-Weinberg

La population « idéale » étudiée dans le cadre du modèle de Hardy-Weinberg doit respecter un certain nombre de conditions (hypothèses) :
  • Une population formée d’individus diploïdes à reproduction sexuée ;
  • Une reproduction entre individus de même génération ;
  • Une rencontre entre individus (et donc des gamètes) liée au hasard ;
  • Une population d’effectif infini (pas de dérive génétique) ;
  • Une absence de mutation du gène considéré ;
  • Une absence de sélection (positive ou négative) du gène considéré ;
  • Une absence de migration des individus de la population.
Dans la plupart des populations réelles, au moins l’une de ces hypothèses ne peut pas être vérifiée et empêche donc de valider le modèle de Hardy-Weinberg.
 
Méthode - Calculer des fréquences alléliques dans une population idéale
Chez une espèce végétale diploïde à floraison annuelle, un gène codant la couleur des fleurs est représenté par 22 allèles :
  • l’allèle AA est à l’origine d’une coloration rouge sang,
  • l’allèle BB d’une coloration rose.
Un échantillon d’individus de la population a été prélevé et la couleur des fleurs déterminée à partir de la concentration des pigments présents. On distingue ainsi 33 types d’individus dont les phénotypes peuvent être annotés de la manière suivante : [rouge], [rose foncé] et [rose].
Dans un échantillon de 416416 individus, on a trouvé 220220 [rouge], 130130 [rose] et 6666 [rose foncé].
On considère que la population respecte le modèle de Hardy-Weinberg.
Calculer les fréquences de chaque allèle du gène codant la couleur des fleurs dans la population étudiée.
 
Conseils
Étape 1 : annoter les génotypes des individus correspondant aux trois phénotypes relevés dans la population végétale.
Étape 2 : donner la relation mathématique décrivant la fréquence de chaque allèle.
Étape 3 : calculer la fréquence de chaque génotype.
Étape 4 : calculer la fréquence de chaque allèle dans la population.
 
Solution
Étape 1 : les organismes sont diploïdes, la correspondance entre les phénotypes et les génotypes sont les suivantes :
  • Phénotype [rose] : génotype (BB) ;
  • Phénotype [rouge] : génotype (AA) ;
  • Phénotype [rose foncé] : génotype (AB) ;
Étape 2 : la population respectant le modèle de Hardy-Weinberg, les fréquences des allèles sont stables au cours des générations. Donc, on a :
f ′(A)=2f′(AA)+f′(AB)2f '(A) = \dfrac{2f'(AA) + f'(AB)}{2}
f′(B)=2f′(BB)+f′(AB)2f'(B) = \dfrac{2f'(BB) + f'(AB)}{2}
Étape 3 : les fréquences des génotypes peuvent être calculées en divisant l’effectif de chaque phénotype par l’effectif total de la population (nota : pour les smartphones, passer en mode paysage si besoin):

f′(AA)=nombre d’individus posseˊdant le pheˊnotype [rouge]nombre total d’individus dans la population=220416=0,5288f'(AA) = \dfrac{\text{nombre d'individus possédant le phénotype [rouge]}}{\text{nombre total d'individus dans la population}} = \dfrac{220}{416}=0,5288

f′(BB)=nombre d’individus posseˊdant le pheˊnotype [rose]nombre total d’individus dans la population=130416=0,3125f'(BB) = \dfrac{\text{nombre d'individus possédant le phénotype [rose]}}{\text{nombre total d'individus dans la population}} = \dfrac{130}{416}=0,3125

f′(AB)=nombre d’individus posseˊdant le pheˊnotype [rose fonceˊ]nombre total d’individus dans la population=66416=0,1587f'(AB) = \dfrac{\text{nombre d'individus possédant le phénotype [rose foncé]}}{\text{nombre total d'individus dans la population}} = \dfrac{66}{416}=0,1587
Vérification : on a bien f′(AA)+f′(BB)+f′(AB)=1f'(AA) + f'(BB)+f'(AB) =1
Étape 4 : les fréquences de chaque allèle sont donc les suivantes :
f ′(A)=2×0,5288+0,15872=0,6082f '(A) = \dfrac{2 \times 0,5288+0,1587}{2}=0,6082
f ′(B)=1−f′(A)=0,3918f '(B) = 1-f'(A)=0,3918
 
Leçon suivante
Autres mécanismes contribuant à la biodiversité