Le tri par sélection, comme le tri par insertion, a un coût quadratique dans le pire cas, mais aussi dans le cas d’une liste presque triée. Il a par contre l’avantage de déplacer moins de valeurs que le tri par insertion.
I. Présentation de l’algorithme
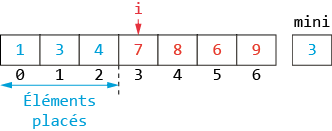
On recherche le plus petit élément et on le met à sa place (en l’échangeant avec le premier). On recherche le second plus petit et on le met à sa place, etc.
Propriétés du tri par insertion :
• tri en place, il n’est pas nécessaire de faire une copie de la liste ;
• tri non stable, deux éléments égaux ne resteront pas nécessairement dans le même ordre.
Exemple standard en Python d’une fonction de tri par sélection :
À noter
En Python, l’échange des cases pourrait être écrit simplement : lst[i], lst[mini] = lst[mini], lst[i].
II. Preuve de correction
Montrons qu’à la fin du tour i de la boucle for, les cases lst[0] à lst[i] incluses sont à leur place définitive.
Au premier tour de boucle (i vaut 0), le plus petit élément est recherché dans toute la liste. Puis il est placé (par échange) dans la case 0.
Supposons qu’à la fin du tour i - 1 tous les éléments de la case 0 à la case i - 1 sont à leur place définitive :
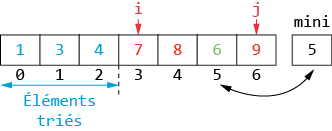
Au début du tour i, on recherche le plus petit élément de la case i à la fin :
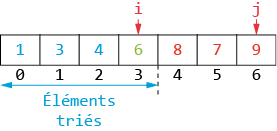
Or toutes ces cases contiennent des valeurs supérieures ou égales à lst[i - 1], puisque les cases 0 à i - 1 sont à leur place. Ce plus petit élément est donc celui qui vient juste après i - 1. Il est donc échangé avec le contenu de la case i. Les éléments d’indices 0 à i sont maintenant à leur place.
Lors du dernier tour de boucle, i vaut len(lst) - 1. À la fin de ce tour, tous les éléments jusqu’à la case len(lst) - 1 incluse sont à leur place définitive. Toute la liste est donc triée.
III. Complexité de l’algorithme
Supposons que la taille de la liste est n.
La boucle for tourne toujours pour i variant de 0 à n−2. Les lignes 4, 9, 10 et 11 s’exécutent en un temps constant (notons le c1), indépendant de n.
La boucle for des lignes 5, 6 et 7 fait varier j de i+1 à n−1 inclus. Elle tourne donc n−1−i fois. Les lignes 6 et 7 s’exécutent en un temps constant, majoré par c2 dans le cas où le test est vérifié.
Le temps d’exécution total est donc :
∑i=0n−2(c1+c2×(n−1−i))=(n−1)c1+c2n(n−1)2=Θ(n2)
Le résultat est un algorithme quadratique dans tous les cas, ce qui est moins bon que le tri par insertion. En revanche, le nombre d’échanges de valeurs est de l’ordre de n.