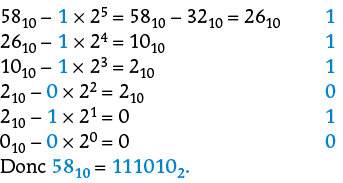Nous sommes habitués à utiliser l’écriture en base 10 des entiers. Mais plus généralement, tout entier peut s’écrire dans une autre base, comme la base 2 ou la base 16, couramment utilisées en informatique car plus adaptées à la mise en mémoire des nombres.
I. Écriture d’un entier en base β
Définition : Une base d’un système de numération positionnel est un entier naturel β supérieur ou égal à deux.
Dire qu’un nombre s’écrit anan−1an−2...a1a0β en base β signifie qu’il est égal à :
an×βn+an−1×βn−1+an−2×βn−2+⋯+a1×β+a0
où les entiers naturels ai sont strictement inférieurs à β.
Exemple : 23710 est égal à 2×102+3×10+7 et 2378=2×82+3×8+7=15910.
À noter
Dans l’écriture 23710 , le 10 en indice indique que le nombre est écrit en base 10.
II. Les bases privilégiées en informatique
En informatique, on travaille en base 2 (les bits), en base 16 (adresses mémoire, couleurs HTML) et parfois en base 8 (droits des fichiers UNIX).
1) Écriture en base 16
Pour écrire un nombre en base 16, il faut disposer d’un caractère pour chacun des entiers de 0 à 15. Or, on ne dispose pas d’assez de chiffres pour écrire les 16 chiffres de la base 16. On complète donc les chiffres de 0 à 9 par les six premières lettres de l’alphabet : A, B, C, D, E et F.
|
Base 10 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
|
Base 16 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
10 |
11 |
2) Écriture en base 2
En base 2, tous les nombres sont représentés avec les deux symboles 0 et 1.
|
Base 10 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Base 2 |
0 |
1 |
10 |
11 |
100 |
101 |
110 |
111 |
1000 |
1001 |
1010 |
Exemple : 11012 est égal à 1 × 23 + 1 × 22 + 0 × 21 + 1 × 20 = 1310.
III. Conversions de la base 10 vers la base 2
1) Algorithme de soustraction
Pour convertir un nombre de la base 10 vers la base 2, on retranche du nombre la plus grande puissance de 2 possible.
Exemple :
À noter
En Python, on utilise des préfixes pour indiquer dans quelle base les nombres sont donnés. 0x pour la base 16, 0b pour la base 2 et 0o pour la base 8.
2) Algorithme de divisions
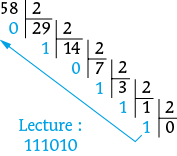
Pour convertir un nombre de la base 10 vers la base 2, on effectue des divisions successives de ce nombre par 2. En lisant les restes de bas en haut on obtient le résultat.
Exemple : 5810 = 1110102.
À noter
On utilise ce même algorithme de la division pour la conversion de la base 10 en n’importe quelle autre base.
IV. Autres conversions
De la base 2 vers la base 16, on groupe les bits par paquets de 4, quitte à rajouter des 0 à gauche.
Exemple : 101010000112 = 0101︸5 0100︸4 0011︸3 = 54316.
De la base 16 vers la base 2, on transforme chaque caractère par un groupe de 4 bits.
Exemple : A3C16 = 1010︸A16=1010 0011︸3 1100︸C16=1210 = 1010001111002.
De la base 16 à la base 10, on écrit les caractères en base 10 et on utilise la définition avec les puissances de la base de départ, ici 16.
Exemple :
À noter
On obtient par le même algorithme la conversion de n’importe quelle base vers la base 10.
A3C16=1010×162+310×161+1210×160=1010×25610+310×1610+1210=2 62010.