Les différentes sources d'erreurs lors d'une mesure
Les différentes sources d’erreurs lors d’une mesure sont :
les conditions expérimentales : la température peut évoluer, la pression peut changer ;
l’imperfection de l’appareil de mesure : des variations peuvent apparaître dans le temps de réponse, l’étalonnage, la sensibilité, la classe de précision, la justesse, la fidélité ;
le défaut de la méthode de mesure : le protocole de mesure est imprécis ou mal adapté ;
les limites de l’opérateur : celui-ci ne refait jamais deux fois la même expérience dans les mêmes conditions (fatigue, erreur de parallaxe, etc.) ;
l’écriture de la valeur du résultat de la mesure d’une grandeur physique, avec un nombre adapté de chiffres significatifs, qui conduit à multiplier les arrondis (voir section 4).
Définition
L’erreur de parallaxe est une erreur de lecture due à la position de l’observateur.
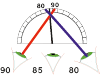
Par conséquent, si l’on effectue N fois la mesure d’une grandeur X, on trouve des valeurs différentes liées à ces erreurs.
Les types d'erreurs de mesure
A) L’erreur aléatoire
Les caractéristiques de l’erreur aléatoires sont :
elle varie pour chaque mesure ;
elle est due aux conditions opératoires ;
elle peut être réduite en augmentant le nombre d’observations.
L’erreur aléatoire affecte la fidélité de mesure, c’est-à-dire l’étroitesse de l’accord entre les valeurs mesurées obtenues par des mesurages répétés du même mesurande dans les mêmes conditions. Autrement dit, une mesure est fidèle si les valeurs mesurées sont peu différentes les unes des autres.
Définition
Mesurande : grandeur que l’on veut mesurer.
Exemple
Lorsque l’on veut mesurer le temps, l’erreur aléatoire vient du fait que le temps de réaction de l’opérateur au départ et à l’arrêt du chronomètre n’est pas toujours le même.
B) L’erreur systématique
Les caractéristiques de l’erreur systématique sont :
elle est identique pour toutes les mesures ;
elle provient d’un appareil mal étalonné, mal utilisé ou défectueux, ou d’une faille dans le protocole de mesure ;
elle peut être éliminée en principe par application d’une correction.
L’erreur systématique affecte la justesse de mesure, c’est-à-dire l’étroitesse de l’accord entre la moyenne d’un nombre infini de valeurs résultant de mesurages répétés et une valeur de référence. Autrement dit, une mesure est juste si l’écart entre la moyenne des résultats et une valeur de référence (ou étalon) est faible.
Exemple
Une balance, plateau vide, indique 0,02 g, ce qui signifie que toutes les mesures vont être surévaluées de 0,02 g.
Les chiffres significatifs
Le nombre de chiffres significatifs (CS) indique la précision d’une mesure physique. Il s’agit des chiffres connus avec certitude, plus le premier chiffre incertain.
Exemple
En fonction du nombre de chiffres significatifs demandés, le nombre 527,397 5 s’arrondit à :
527,398 avec 6 chiffres significatifs ;
527,40 avec 5 chiffres significatifs ;
527,4 avec 4 chiffres significatifs ;
527 avec 3 chiffres significatifs.
Les règles pour compter les chiffres significatifs sont :
on ne prend pas en compte les zéros à gauche du nombre. En revanche, un zéro à droite d’un nombre est toujours significatif, même après une virgule ;
dans le cas d’une valeur écrite sous la forme a × 10n, seuls les chiffres qui composent l’écriture de a sont significatifs.
Exemples
12,43 comprend 4 CS.
0,0354 comprend 3 CS.
3,00 × 108 comprend 3 CS.
Lors d’un calcul, tous les chiffres significatifs sont pris en compte : les résultats intermédiaires peuvent donc dépasser le nombre de chiffres significatifs, et seul le résultat final est écrit avec le nombre correct de chiffres significatifs.
Lorsqu’on a plusieurs grandeurs avec un nombre de chiffres significatifs différents, le résultat sera exprimé avec le plus petit nombre de chiffres significatifs.
