L’étude d’une projection orthogonale débouche sur des questions de distance d’un point à une droite, et en particulier aux tangentes à un cercle passant par un point donné.
I Définition
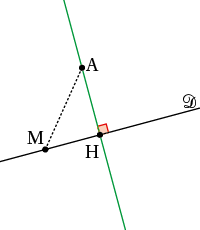
On considère une droite 𝒟 et un point A. On trace la perpendiculaire à 𝒟 passant par A. Elle coupe 𝒟 en H. Le projeté orthogonal de A sur 𝒟 est le point H.
La distance AH est la distance de A à la droite 𝒟.
Remarques : • Le point H est le point de 𝒟 qui est le plus proche de A. En effet si M ∈ 𝒟, alors AM ⩾ AH.
• Si A est un point de 𝒟, alors son projeté orthogonal sur 𝒟 est A lui-même.
II Applications
1 Généralisation du théorème de Thalès
Deux points A et B ont pour projetés orthogonaux sur la droite ∆ les points A′ et B′. Soit M un point du segment ]AB[ et M′ son projeté orthogonal sur ∆. Alors :
En effet, soit 𝒟 la parallèle à (AB) passant par A′. Dans les parallélogrammes AMNA′ et ABCA′ on a AM = A′N et AB = A′C.
Le théorème de Thalès dans les triangles A′NM′ et A′CB′ donne : .
Remarques : • Cette propriété se généralise dans le cas où M est sur la droite (AB) en dehors de [AB].
• Le projeté orthogonal du milieu d’un segment est le milieu du projeté orthogonal de ce segment.
2 Tangente à un cercle en un point du cercle
Soit A un point d’un cercle de centre O et de rayon R. La tangente au cercle en A est la droite ∆ dont la distance à O est égale à R.
Méthode
1 Déterminer un ensemble de points
Repère
ConseilsUtilisez une propriété des triangles rectangles.
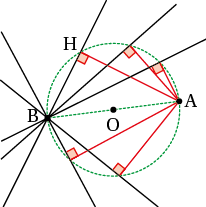
On donne deux points A et B. On trace des droites passant par B. Sur quelle figure géométrique se trouvent les projetés orthogonaux de A sur chacune de ces droites ?
solutionAppelons H un projeté orthogonal de A sur une droite. Le triangle AHB est rectangle donc H appartient au cercle de diamètre [AB] qui est le cercle circonscrit à ce triangle. Tous les projeté orthogonaux appartiennent donc à ce cercle.
2 Construire une tangente à un cercle
On considère un cercle 𝒞 de centre O et de rayon R, et A un de ses points. On veut construire la tangente à 𝒞 passant par A, c’est-à-dire la droite située à la distance R du centre du cercle. La figure 1 montre les conditions initiales.
a. Donner le programme de construction de la figure 2.
b. Que représente la droite bleue pour le segment noir dans la figure 3 ?
c. Pourquoi le problème est-il résolu à l’étape 3 ?
conseilS
b. Les deux arcs de cercle en pointillé sont centrés enO et enM.
c. La distance d’un pointP à une droite est la distancePH oùH est le point d’intersection de la droite avec sa perpendiculaire passant parP.
solutiona. Construire la droite (OA) puis tracer le cercle de centre A passant par O. Il coupe la droite (OA) en M.
b. La droite tracée est la médiatrice du segment [MO].
c. La distance de O à la droite bleue est égale à OA c’est-à-dire à R. C’est bien la tangente cherchée.