Position relative de deux courbes

La position relative de deux courbes se résume à l’étude du signe de la différence des ordonnées de deux points de même ­abscisse de ­chacune des deux courbes. Cette étude permet, en ­économie, d’estimer un bénéfice.

I. Définition

Étudier la position relative de deux courbes 𝒞₁ et 𝒞₂ revient à savoir sur quel intervalle 𝒞₁ est au-dessus (respectivement en dessous) de 𝒞₂.

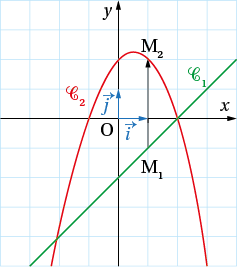
Exemple : Sur le graphique ci-dessous, on voit que sur [–2 ; 2] l’ordonnée de M₂ est supérieure à celle de M₁ on peut donc en déduire que 𝒞₁ est en dessous de 𝒞₂.

Les fonctions $f_1$ et $f_2$ sont définies par $f_1(x)=x-2$ et $f_2(x)=-x^2+x+2$.

II. Propriétés

Soit 𝒞₁ et 𝒞₂ les courbes représentatives de deux fonctions f₁ et f₂. On considère deux points $M_1$ et $M_2$ de même abscisse $x$ appartenant respectivement à 𝒞₁ et 𝒞₂, leurs ordonnées respectives sont donc $f_1(x)$ et $f_2(x)$.

•  𝒞₁ est au-dessus de 𝒞₂ si et seulement si $f_1(x)\ge f_2(x)$ ou encore $f_1(x)-f_2(x)\ge 0$.

•  𝒞₁ est en dessous de 𝒞₂ si et seulement si $f_1(x)\le f_2(x)$ ou encore$f_1(x)-f_2(x)\le 0$.

•  𝒞₁ et 𝒞₂ se croisent si et seulement si $f_1(x)=f_2(x)$.

Exemple : On peut retrouver le résultat obtenu graphiquement précédemment en faisant l’étude du signe de la différence $f_1(x)-f_2(x)$.

On a alors :

$f_1(x)-f_2(x)= x-2-(-x^2+x+2)$.

${\phantom{f_1(x)-f_2(x)}= x^2-4}$

${\phantom{f_1(x)-f_2(x)}= (x-2)(x+2)}$.

On obtient un polynôme du second degré dont les racines sont –2 et 2. On en déduit que cette différence est négative entre les racines, c’est-à-dire sur [–2 ; 2] et positive à l’extérieur des racines, c’est-à-dire sur ]–∞ ; –2[ et ]2 ; +∞[.

𝒞₁ est donc en dessous de 𝒞₂ sur [–2 ; 2] et au-dessus sur ]–∞ ; –2[ et ]2 ; +∞[.

Méthode

Étudier la position relative de deux courbes

Conseil

Étape 1. Pour comparer les ordonnées de deux points de même abscisse x, l’un appartenant à𝒞_f et l’autre à𝒞_g , on calcule $f(x)-g(x)$.

Étape 2. On étudie le signe de cette différence.

Soient f et g les fonctions définies sur ℝ par :

$f(x)=-2x^2-x+5$ et $g(x)=-x+1$.

On appelle 𝒞_f et 𝒞_g leurs courbes représentatives.

Étudier la position relative de ces deux courbes sur ℝ.

Solution

Étape 1. Déterminons la différence :

$f(x)-g(x)= (-2x^2-x+5)-(-x+1)$

${\phantom{f(x)-g(x)}=-2x^2-x+5+x-1}$

${\phantom{f(x)-g(x)}=-2x^2+4}$

Étape 2. Étudions alors le signe de $f(x)-g(x)= -2x^2+4$

Les racines de l’équation du second degré $-2x^2+4= 0$ sont $x=\sqrt 2$ et $x=-\sqrt 2$.

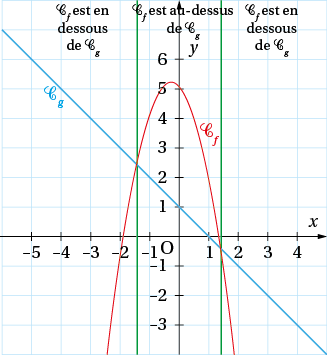
Donc $-2x^2+ 4$ est positif sur $[-\sqrt 2~;~\sqrt 2]$ et négatif sur $]-\infty ~;~-\sqrt 2[ \cup ]\sqrt 2~;~+\infty[$. Ainsi :

– si $x\in [-\sqrt 2~;~\sqrt 2]$, $f(x)\ge g(x)$ et la courbe représentant f est située ­au-­dessus de celle représentant g ;

– si $x\in ]-\infty ~;~-\sqrt 2[ \cup ]\sqrt 2~;~+\infty[$, $f(x)\le g(x)$ et la courbe représentant f est située en dessous de celle représentant g.

Vérifiez que vous avez bien compris les points clés des fiches 17 à 19.