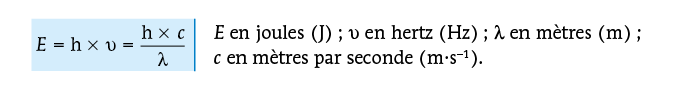Le domaine de l’infiniment petit est décrit par la mécanique quantique : le photon est la particule constitutive de la lumière, et l’atome possède une énergie qui est quantifiée.
I. La nature corpusculaire de la lumière
En 1905, le physicien allemand Albert Einstein émet l’hypothèse que la lumière peut être décrite non pas comme une onde, mais comme constituée de petites particules de lumière appelées photons.
Les photons sont les particules constitutives de la lumière. Ils ont une masse nulle et se déplacent à la vitesse de la lumière. Chaque photon porte une énergie E qui dépend de la fréquence υ de la radiation lumineuse ou de la longueur d’onde λ de la radiation :
h est la constante de Planck exprimée en joules-secondes : h = 6,626 × 10−34 J·s.
II. La quantification de l’énergie des atomes
En 1913, le physicien Danois Niels Bohr est le premier à affirmer que : « L’atome ne peut exister que dans certains états d’énergie bien définis. » C’est la quantification de l’énergie des atomes. À chaque état est associée une énergie (notée E) : on dit que l’atome est dans le niveau d’énergie E.
L’électronvolt (eV) est une unité d’énergie adaptée à la mécanique quantique :
1 eV = 1,602 × 10−19 J.
À noter
On utilise aussi les multiples de l’électronvolt : 1 keV = 103 eV = 1,602 × 10−16 J ;
1 Mev = 106 eV = 1,602 × 10−13 J ; 1 GeV = 109 eV = 1,602 × 10−10 J.
Méthode
Exploiter un diagramme d’énergie
Le diagramme d’énergie de l’atome d’hydrogène est donné ci-contre.
a. Quelle est l’énergie, en électronvolts, de l’état fondamental ?
b. Quelle est l’énergie, en joules, du 2e état excité ?
c. L’atome, initialement dans son état fondamental, passe dans son 3e niveau d’énergie. Calculer la variation ΔE en énergie de l’atome, sachant que 1 eV = 1,602 × 10−19 J.
d. L’atome, initialement dans son 4e niveau d’énergie, passe dans son 1er niveau d’énergie. Calculer la variation ΔE en énergie de l’atome.
Conseils
a. Rappelez-vous la définition de l’état fondamental.
b. Appliquez la conversion : 1 eV = 1,602 × 10−19 J.
Attention, le 2e état excité correspond au 3e niveau d’énergie.
c et d. Calculez la différence d’énergie entre le niveau d’arrivée et celui de départ. Une variation correspond à la différence entre un état final et un état initial.
Solution
a. L’état fondamental est l’état de plus basse énergie. On trouve donc pour son énergie par lecture graphique :
E0 = −13,6 eV.
Les énergies sont souvent comptées négativement.
b. Le 2e état excité correspond au 3e niveau d’énergie.
On lit l’énergie en électronvolts associée :
E2 = −1,51 eV.
On convertit en joules :
E2 = −1,51 × 1,602 × 10−19 J = −2,42 × 10−19 J.
c. On exprime la variation d’énergie ΔE :
ΔE = E2 – E0 = −1,51 − (−13,6) = 12,1 eV.
d. On exprime la variation d’énergie ΔE :
ΔE = E0 – E3 = −13,6 − (−0,85) = −12,8 eV.