Minimiser les transferts thermiques pour économiser de l'énergie

La résistance et la conductance thermiques

A) Définitions

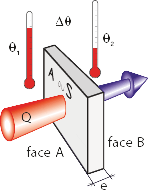
La résistance thermique désigne la résistance d’un élément au passage d’un flux de conduction thermique. On parle aussi de résistance surfacique dans le cas d’une paroi plane. Elle se calcule avec la formule :

R = $\frac{\text{e}}{\lambda \text{.S}}$, avec e l’épaisseur de la paroi en m, S la surface en m² et λ la conductivité du matériau en W/m/K ou W/m/°C.

Son unité est le K/W ou °C/W. Les fabricants d’isolants indiquent la valeur de la résistance thermique ramenée à une surface de 1 m². Elle est alors exprimée en m².K.W^-1.

La conductance thermique, notée UA, quantifie l’aptitude d’un matériau à conduire la chaleur et est définie comme l’inverse de la résistance thermique. Elle dépend de la surface, de l’épaisseur et de la conductivité thermique de l’élément considéré. Son unité est le watt par kelvin (W.K^-1 ou W/K) ou le watt par degré Celsius (W/°C) et sa formule de calcul est :

UA = $\frac{\lambda \text{.S}}{\text{e}}$ = $\frac{\text{1}}{\text{R}}$.

B) Calcul

On veut comparer les conductances de deux plaques, l’une en verre, l’autre en altuglas® (du polyméthacrylate de méthyle, ou PPMA). On va calculer pour cela les résistances thermiques.

Les données fabricant sont les suivantes : λ_verre = 1 W/m/°C et λ_altuglas = 0,17 W/m/°C.

Les épaisseurs des deux plaques sont e_verre = 10 mm et e_altuglas = 4 mm.

On calcule la résistance thermique de chaque plaque :

R_verre = $\frac{\text{e}}{{\lambda }_{verre}}$ = $\frac{\text{0,01}}{\text{1}}$ = 0,01 m².°C/W. 

R_altuglas = $\frac{\text{e}}{{\lambda }_{\text{altuglas}}}$ = $\frac{\text{0,004}}{\text{0,17}}$ = 0,0235 m².°C/W.

Le matériau le plus isolant est donc l’altuglas, par conséquent la meilleure conductance est celle du verre.

La puissance thermique

A) Définition

La puissance thermique ou flux thermique, notée Φ, désigne la quantité de chaleur Q (ou transfert thermique) traversant une surface isotherme par unité de temps. Elle se calcule avec la formule :

Φ = $\frac{\text{Q}}{\text{t}}$ , avec Φ en watt (W), Q en joules (J) et t en seconde(s).

Si les températures θ₁ et θ₂ restent constantes dans le temps, on peut aussi écrire :

Φ = $\frac{{\theta }_{\text{1}}-{\theta }_{\text{2}}}{\text{R}}$ avec R la résistance thermique de la paroi (K/W ou °C/W).

Les autres unités utilisées sont la calorie par heure (cal/h) ou la thermie par heure (th/h).

B) Calcul

On envisage la puissance thermique à travers une porte séparant deux pièces, dont l’une est maintenue à la température θ₁ de 21 °C et l’autre est maintenue à la température θ₂ de 19 °C.

Cette porte, en pin maritime, a une épaisseur de 4 cm. Elle mesure 2,045 m de hauteur pour 0,83 m de largeur. Sa surface est donc :

S = 2,045 × 0,83 = 1,6932 m².

La conductivité thermique du pin maritime est : λ = 0,150 W.m^-1.K^-1.

La résistance thermique du pin est : R = $\frac{\text{e}}{\lambda }$ = $\frac{\text{0,04}}{\text{0,15}}$ = 0,2667 m².°C/W.

La puissance thermique Φ sera : Φ = $\frac{\text{S}\times \left({\theta }_{\text{2}}-{\theta }_{\text{1}}\right)}{\text{R}}$× = 1,6932 × $\frac{2}{\mathrm{0,2667}}$ ≈ 12,697 W.