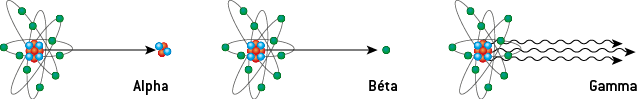Légende de la leçon
Vert : définitions
I. Le diagramme d’état d’un corps pur
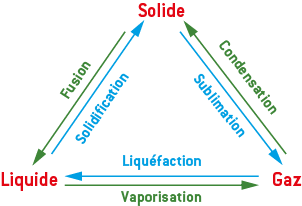
1) Les changements d’état
Le changement d’état d’un corps est une transformation physique au cours de laquelle le corps passe d’un état physique à un autre.
Un corps pur est un corps constitué d’une seule espèce chimique, contrairement à un mélange. Sous une pression donnée, le changement d’état d’un corps pur se fait à une température constante, caractéristique de ce corps pur. Cette température est appelée température de changement d’état.
2) Les diagrammes d’état
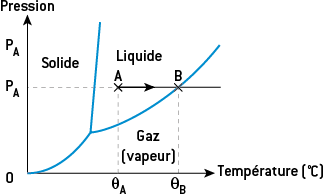
Connaissant sa température et sa pression, on peut prévoir l’état physique d’un corps pur en utilisant son diagramme d’état, qui est une représentation graphique en deux dimensions (pression en fonction de la température). On peut y voir trois lignes, qui représentent les frontières entre l’état solide, l’état liquide et l’état gazeux.
Dans le cas de l’eau, les changements d’état correspondent à des ruptures (lors de la vaporisation) ou à l’établissement (lors de la liquéfaction) de liaisons hydrogène entre les molécules d’eau.
Exemple
Soit un corps pur dont le diagramme d’état est ci-contre. Il est initialement à la pression PA et à la température θA. D’après le diagramme, ce corps pur est à l’état liquide. On le chauffe à pression constante. Sa température augmente jusqu’au point B situé à la frontière entre l’état liquide et l’état gazeux. Au point B, le corps se vaporise à la température θB, qui est la température de vaporisation de ce corps pur à la pression PA. Dès lors, si l’on poursuit le chauffage, le corps pur est entièrement à l’état gazeux et sa température augmente.
3) Les énergies massiques de changement d’état
Pendant un changement d’état de l’état 1 vers l’état 2, la variation d’énergie est égale à l’énergie thermique échangée avec le milieu extérieur. Elle dépend de la masse m du corps pur et de l’énergie massique de changement d’état L1→2 du corps pur :
m : la masse en kilogramme
Q = m × L1→2 L1→2 : l’énergie massique de changement d’état en joule par kilogramme (J.kg−1)
Q : l’énergie thermique échangée en joule (J)
Remarque
Il faut préciser le changement d’état considéré :
- le corps pur reçoit de l’énergie (L1→2 > 0) lors d’une fusion, d’une vaporisation ou d’une sublimation (passage vers un état moins organisé) ;
- inversement, le corps pur cède de l’énergie (L1→2 < 0) lors d’une condensation, d’une liquéfaction ou d’une solidification (passage vers un état plus organisé).
LS→L = – LL→S ; LL→G = – LG→L ; LS→G = – LG→S.
Exemple
On fait fondre une masse m = 45 g = 0,045 kg de glaçons à 0 °C. LS→L = 334 kJ.kg–1.
Les glaçons vont recevoir une énergie Q = m × LS→L = 0,045 × 334 = 15 kJ.
4) La variation d’énergie lors d’une variation de température
Lorsque la température d’un matériau dans un seul état physique passe de la température initiale Ti à la température finale Tf, il se produit un échange d’énergie thermique Q avec le milieu extérieur.
Q est proportionnelle à la différence de température (Tf – Ti), à la masse m de phase condensée et à la capacité thermique massique c de la phase condensée (plus c est grande, moins la variation de température est élevée pour une même masse) :
Exemple
L’eau liquide produite par la fonte des glaçons à 0 °C provient d’un gain d’énergie de 3,0 kJ. ceau = 4,2 J.g–1.K–1.
On peut alors calculer la température finale de l’eau.
La formule Q = m × ceau × (Tf – Ti) permet d’écrire (Tf – Ti) = Q/m × ceau.
Soit Tf = Ti + Q/m × ceau = 0 + 3,0 × 103/(45 × 4,2) = 16 °C.
Remarque
Lorsqu’un corps reçoit de l’énergie thermique du milieu extérieur, son énergie augmente, ce qui se traduit soit par une élévation de température, soit par un changement d’état, soit par une élévation de température et un changement d’état.
II. La radioactivité
La radioactivité est la désintégration de noyaux atomiques instables. Un noyau radioactif se décompose spontanément en un noyau fils différent avec émission de particule ou de rayonnement. La radioactivité peut être naturelle ou artificielle, lorsque c’est l’homme qui a créé les radioisotopes.
1) Les quatre types d’émissions radioactives
Trois sont des émissions de particules de matière :

Le rayonnement gamma (γ) est de nature électromagnétique : il est constitué de photons. Les rayonnements γ ont une fréquence comprise entre 3 × 1019 Hz et 3 × 1022 Hz, ce qui correspond à une longueur d’onde dans le vide λ0 comprise entre 10−11 et 10−14 m. Les rayons gamma ont des longueurs d’onde plus petites que les rayons X, et donc des fréquences plus grandes : ils sont produits par désintégration radioactive, contrairement aux rayons X.
2) L’écriture d’une réaction nucléaire : lois de conservation
Les équations de décomposition sont régies par les lois de conservation de Soddy, selon lesquelles, au cours de toute réaction nucléaire, il y a :
- conservation du nombre de charge : la somme des numéros atomiques à gauche est égale à celle à droite dans l’équation nucléaire (Σ Z1 = constante) ;
- conservation du nombre de masse ou de nucléons : la somme des nombres de masse à gauche est égale à celle à droite dans l’équation nucléaire (Σ A1 = constante).
Les équations nucléaires de décomposition sont données dans le tableau suivant :

Lors d’une réaction nucléaire α ou β, le noyau formé est initialement dans un état « excité », à cause du bouleversement important suscité par l’éjection de la particule α ou β. Le noyau retrouve son état fondamental en émettant l’excès d’énergie sous forme de radiations ou photon γ : XZA* → XZA + nγ.
Exemple
Un radioisotope U92238 (uranium 238) se décompose en N93238p (neptunium 238).
L’équation nucléaire est : U92238→XZA+N93238p. Pour trouver le rayonnement émis, on utilise les lois de Soddy : 238 = A + 238 et 92 = Z + 93, ce qui permet de trouver A = 0 et Z = –1.
Le rayonnement émis est donc X−10. C’est un électron, il s’agit donc de radioactivité β–.
III. L’évolution de la population moyenne d’un ensemble de noyaux radioactifs
1) La loi de décroissance radioactive
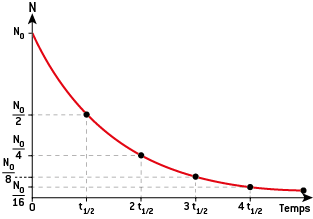
Le nombre noyaux radioactifs diminue au cours du temps selon une loi mathématique :
2) La demi-vie radioactive t½
On appelle demi-vie radioactive t1/2(ou période) le temps au bout duquel la moitié du nombre de noyaux initialement présents s’est désintégrée.
Au bout d’une demi-vie, l’activité est divisée par 2 : N= N02. Après 2 demi-vies, l’activité est à nouveau divisée par 2, soit 4 depuis le début : N = N04 = N022.
Les demi-vies radioactives sont très différentes d’un élément radioactif à un autre et même d’un isotope radioactif à un autre. La décroissance radioactive du tritium H13 est trois cents millions de fois plus rapide que celle de l’uranium 235. Voici quelques exemples de radionucléides et leur demi-vie :

3) La relation entre la demi-vie radioactive t½et la constante de temps τ
Lorsque le temps écoulé est égal au temps de demi-réaction, alors N = N0/2 et donc Ln N N0 = –t½/λ,soit Ln 1 2 = –t½/τ ou τ × Ln 2 = t½. Le temps de demi-réaction ne dépend pas de la concentration initiale en réactif. t½ et τ s’expriment tous les deux en seconde.
4) L’activité
L’activité A au temps t est le nombre de désintégrations par unité de temps. Elle est mesurée avec un compteur Geiger-Müller. Elle dépend du nombre de noyaux présents et du radionucléide. Elle s’exprime en becquerel (Bq) : un becquerel correspond à une désintégration par seconde.
IV. Les réactions nucléaires
1) Les réactions de fusion et de fission
Lors d’une réaction de fusion, deux noyaux ayant un petit nombre de masse fusionnent pour produire un noyau ayant un plus grand nombre de masse.
Exemples : H12 + H12 → H13 + H11
H12 + H13 → H24e + n01
Lors d’une réaction de fission, on bombarde un noyau ayant un grand nombre de masse avec un neutron pour le casser en produisant alors deux noyaux de nombres de masse plus petits et deux à trois neutrons (qui pourront alors casser d’autres gros noyaux et engendrer une réaction en chaîne).
Exemple : U92235 + n01 → Z4091r + C58142e + 3 n01 + 6 e−10
2) Le défaut de masse et l’énergie libérée au cours d’une réaction nucléaire
Au cours d’une réaction nucléaire spontanée, il y a diminution de la masse globale du système. Pour calculer la masse Δm ayant disparu au cours d’une réaction nucléaire, il faut calculer la différence entre la somme des masses des produits et la somme des masses des réactifs. Cette variation Δm est négative puisque la masse du système diminue.
Δm = Σ mproduits – Σ mréactifs.
Exemple
Le radium 226 se décompose spontanément en radon 222 par radioactivité α selon la réaction : 226Ra → 222Rn + 4He.
On a m(226Ra) = 3,7524385 × 10–25 kg, m(222Rn) = 3,6859056 × 10–25 kg et m(4He) = 0,0664467 × 10–25 kg.
La masse des noyaux avant désintégration est Σ mréactifs = 3,7524385 × 10–25 kg.
La masse des noyaux après désintégration est Σ mproduits = 3,6859056 × 10–25 + 0,0664467 × 10–25= 3,7523523 × 10–25 kg.
Au cours de cette désintégration alpha, il n’y a pas conservation de la masse. La variation de masse vaut Σ mproduits – Σ mréactifs = –8,62 × 10–30 kg.
L’énergie libérée ΔE est calculée en utilisant la relation d’Einstein :
Exemple
L’énergie libérée pour chaque noyau de radium 226 qui se désintègre est :
ΔE = |Δm| × c2 = |8,62 × 10–30| × (3,00 × 108)2 = 7,76 × 10–13 J.
Cette énergie peut aussi s’exprimer en électronvolt, avec 1 eV = 1,60 × 10–19 J. Dans ce cas, l’énergie vaut donc : E = 7,76 × 10–13/1,60 × 10–19 = 4,85 MeV.
Remarque
Les énergies mises en jeu dans le domaine nucléaire sont environ un million de fois plus grandes que dans le domaine des liaisons chimiques.