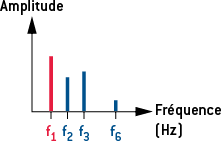Légende de la leçon
Vert : définitions
I. Le spectre d’amplitude d’un son
1) Son pur et son complexe
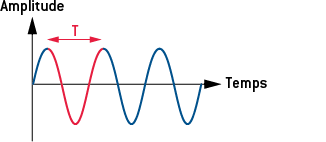
Un son pur a une représentation temporelle de nature sinusoïdale et donc un spectre d’amplitude contenant une raie de fréquence égale à celle du son.
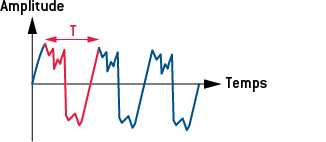
Un son complexe est un son périodique qui est la somme de signaux sinusoïdaux : son spectre d’amplitude contient donc plusieurs raies de fréquences égales à des multiples de la fréquence la plus petite, qui est la fréquence fondamentale (égale à celle du son).
La hauteur d’un son pur ou complexe est sa fréquence en hertz (Hz), c’est donc la valeur de la fréquence fondamentale f1 et c’est aussi l’inverse de la période T en seconde (s).
2) Le timbre d’un son
Lorsque deux instruments de musique différents jouent la même note (même fréquence f1), on ne perçoit pas le même son alors que la fréquence de la note jouée est la même : ils ont un timbre différent. Les deux sons ont des spectres d’amplitude différents avec la même fréquence fondamentale.
Exemple
Le spectre en amplitude du mi4 (660 Hz) pour une guitare (à gauche) et pour une flûte (à droite). Les deux sons ont bien la même hauteur (660 Hz) puisque la même note est jouée. Cependant, celui de la guitare est plus riche en harmoniques : il sera perçu différemment.
II. L’intensité acoustique I et le niveau sonore L
1) La relation entre les deux grandeurs

Sonomètre
L’intensité acoustique I est mesurée en watt par mètre carré (W.m–2) : c’est une puissance par unité de surface. L’intensité de référence, par rapport à laquelle sont mesurés les sons, est fixée à I0 = 1,0 × 10–12 W.m–2.
Les intensités sonores s’ajoutent. Ainsi, en un point, deux sons d’intensités sonores I1 = 7,0 × 10–4 W.m–2 et I2 = 4,0 × 10–4 W.m–2 donnent une intensité I = I1 + I2 = 1,1 × 10–3 W.m–2.
Le niveau sonore L (level en anglais) s’exprime en décibel (dB). C’est une échelle subjective, car elle ne prend pas en compte la sensibilité de l’oreille, qui dépend de la fréquence. Le niveau sonore est lié à l’intensité acoustique par la formule L = 10 log II0. Il est mesuré avec un sonomètre. Les niveaux sonores ne s’ajoutent pas !
Exemple
Un instrument de musique produit un son dont l’intensité acoustique vaut I = 5,0 × 10–4 W.m–2.
Pour calculer le niveau sonore correspondant, on utilise la formule L = 10 log II0 = 10 log 5,0×10−41,0×10−12 = 87 dB.
Lorsque l’intensité acoustique est multipliée par 10, alors le niveau sonore augmente de 10 dB. Lorsque l’on passe d’un niveau sonore de 50 dB à 70 dB, cela veut donc dire que l’intensité sonore a été multipliée par 100.
Pour déterminer l’intensité acoustique à partir du niveau sonore, il faut transformer la formule pour obtenir I = I0 10L/10.
Exemple
Un klaxon émet un bruit dont le niveau sonore vaut L = 75 dB à 20 m.
L’intensité acoustique est calculée avec la formule I = I0 10L/10 = 1,0 × 10–12 × 1075/10 = 3,2 × 10–5 W.m–2.
2) L’oreille humaine
a) Les seuils de perception
La valeur 0 dB correspond au seuil d’audibilité, c’est-à-dire la valeur la plus faible pouvant être perçue par une oreille humaine. Cette valeur a été définie en réalisant des expériences avec un son de fréquence 1 000 Hz. L’intensité sonore correspondante vaut 10–12 W.m–2 (c’est l’intensité de référence).
Le seuil de douleur est de 130 dB. Cependant, l’oreille peut subir des traumatismes à partir de 80 dB. La législation sur le bruit au travail impose l’utilisation de protections auditives ou limite l’exposition à des niveaux sonores pendant des durées déterminées.

Échelle des niveaux sonores
La perception de l’oreille humaine augmente avec la fréquence pour être maximale vers 3 à 4 kHz ; elle diminue ensuite rapidement.
b) Le contrôle de l’audition
Avec l’âge, les sons ayant une fréquence supérieure à 12 kHz sont moins bien perçus et deviennent parfois inaudibles. On peut faire un bilan d’audition et obtenir un audiogramme, qui permet de mesurer la capacité auditive d’une personne. Il est basé sur des sons purs à fréquences choisies, pour lesquelles on mesure le seuil de l’audition. À l’aide d’un casque, on adresse à une oreille les différentes fréquences en augmentant le niveau sonore : lorsque le patient entend un son, il prévient le médecin.
Les différents résultats sont placés sur un graphe et comparés au seuil normal d’audition pour les mêmes fréquences afin de déterminer le déficit auditif du patient. La courbe rouge correspond à l’oreille gauche et la courbe bleue à l’oreille droite. L’audiogramme de gauche correspond à une personne entendant normalement alors que celui de droite est celui d’une personne présentant une déficience auditive.
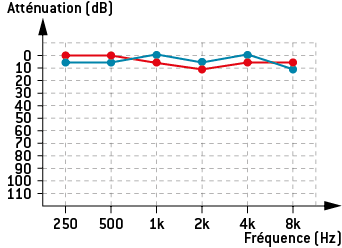
Personne entendante
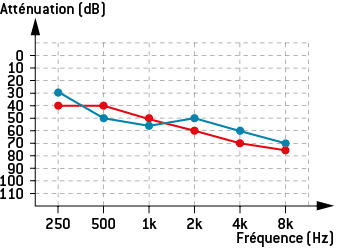
Personne avec une déficience auditive

III. La transmission et l’absorption des ondes sonores
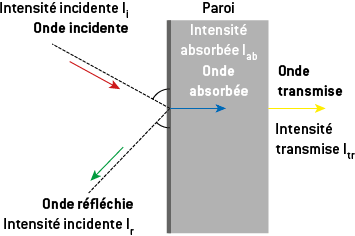
Lorsqu’une onde sonore se propageant dans un premier milieu rencontre un milieu différent, une partie de l’énergie est transmise, une partie est absorbée par le matériau et le reste est réfléchi.
On définit alors les coefficients correspondants sans unité :
- coefficient de transmission : t = Itr Ii;
- coefficient d’absorption : a = Iab Ii.
Les phénomènes de transmission et d’absorption sont facilement mis en évidence en utilisant un sonomètre avant et après un obstacle.
Certains matériaux absorbent fortement les sons en ayant des coefficients de valeur d’absorption proches de 1. Dans les immeubles, il faut surtout limiter la transmission et avoir des coefficients de transmission faibles, inférieurs à 10–3.