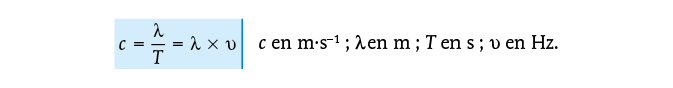La lumière, les rayons X, les rayons ultraviolets, le rayonnement infrarouge sont tous des ondes électromagnétiques. Un tel rayonnement est caractérisé par sa célérité, sa fréquence et sa longueur d’onde.
I. Les caractéristiques d’une onde électromagnétique
Une onde électromagnétique est une vibration électrique et magnétique qui se propage de proche en proche. Elle transporte de l’énergie, mais pas de matière.
À noter
Toutes les ondes électromagnétiques (lumière visible, rayons X…) possèdent la même célérité dans le vide.
Elle se propage dans le vide et les milieux matériels transparents. Sa célérité c dépend du milieu dans lequel elle se propage. Dans le vide :
c = 299 7924858 m· s–1 ≈ 3,00 × 108 m· s–1
|
Milieu |
air |
eau |
diamant |
|
c (m·s–1) |
3,00 × 108 |
2,25 × 108 |
1,25 × 108 |
Une onde électromagnétique est périodique à la fois dans le temps et dans l’espace. Elle est caractérisée par sa longueur d’onde λ (période spatiale) exprimée en mètres et par sa période temporelle T exprimée en secondes.
La fréquence et la période sont liées par la relation : υ=1T⇔T=1υ
Célérité, longueur d’onde et période (ou la fréquence) sont liées par la relation :
II. Les différents domaines des ondes électromagnétiques
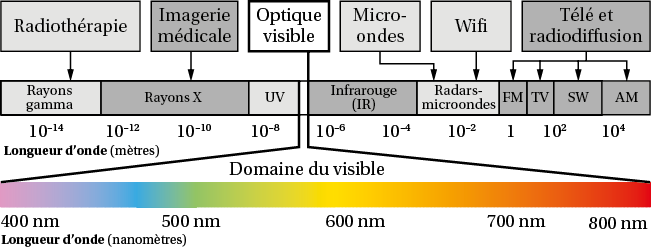
En fonction de la valeur de sa longueur d’onde, une onde électromagnétique appartient à un domaine spécifique et correspond à un usage spécifique.
Méthode
Calculer la fréquence d’une onde électromagnétique à partir de sa longueur d’onde
Le spectre de la lumière blanche est donné ci-dessous.
a. Déterminer l’intervalle en fréquences des radiations visibles.
b. Une radiation verte possède-t‑elle une fréquence inférieure à celle d’une radiation jaune ?
Conseils
a. Utilisez la conversion : 1 nm = 1 × 10−9 m.
À partir de la formule c = λ × υ, exprimez la fréquence puis calculez-la.
La célérité de la lumière dans le vide doit être connue : c ≈ 3,00 × 108 m· s–1.
b. Identifiez le type de relation mathématique existant entre la longueur d’onde et la fréquence à partir de la formule c = λ × υ.
Solution
a. On convertit les valeurs extrêmes des longueurs d’onde en mètres :
800 nm = 800 × 10–9 m = 8,00 × 10–7 m et 400 nm = 4,00 × 10–7 m.
On exprime la fréquence en fonction de la célérité et de la longueur d’onde :
c=λ×υ⇔υ=cλ.
On calcule les fréquences associées aux longueurs d’onde extrêmes :
υ=cλ=3,00×1084,00×10–7=7,50×1014 Hz;
υ=cλ=3,00×1088,00×10–7=3,75×1014 Hz.
L’intervalle en fréquence est donc : [3,75 × 1014 Hz ; 7,50 × 1014 Hz].
b. D’après la formule trouvée à la question a, la fréquence et la longueur d’onde sont des grandeurs inverses : si l’une augmente alors l’autre diminue. La longueur d’onde associée à une radiation verte étant de l’ordre de 500 nm et celle d’une radiation jaune de l’ordre de 600 nm, on en déduit qu’une radiation verte possède une fréquence supérieure à celle d’une radiation jaune.