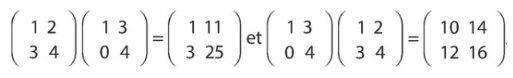I. Notion de matrice
Définition :
Une matrice A de dimension n×p est un tableau à n lignes et p colonnes, composé de nombres réels, appelés coefficients de la matrice.
 De façon générale, on note A=(aij), aij étant le coefficient situé à la i-ème ligne et j-ème colonne.
De façon générale, on note A=(aij), aij étant le coefficient situé à la i-ème ligne et j-ème colonne.
L’ensemble des matrices de dimension n×p est noté Mn,p(R).
Matrices égales :
Deux matrices A=(aij) et B=(bij) de même dimension n×p sont égales si, et seulement si : aij=bij pour tout i∈{1;2;…;n} et j∈{1;2;…;p}
II. Du vocabulaire
Matrices transposées : Soit A=(aij) une matrice de dimension n×p. La matrice transposée de A est la matrice At de dimension p×n :
At=(aji). Les lignes de A correspondent aux colonnes de At. | Exemples : 
|
Matrice ligne : Une matrice de dimension 1×p est appelée matrice ligne. |  est une matrice ligne est une matrice ligne
|
Matrice colonne : Une matrice de dimension n×1 est appelée matrice colonne. |  est une matrice colonne est une matrice colonne
|
Matrice carrée : Une matrice de dimension n×n est appelée matrice carrée d’ordre n. |  est une matrice est une matrice
carrée d'ordre 2 |
Matrice diagonale : Une matrice diagonale d’ordre n est une matrice carrée d’ordre n telle que tous ses coefficients hors de la diagonale principale valent 0. |  est une matrice diagonale est une matrice diagonale
d'ordre 3 |
III. Somme de matrices et produit par un réel
∘ Somme de deux matrices :
Deux matrices A=(aij) et B=(bij) sont sommables si, et seulement si, elles ont la même dimension.
Alors A+B=(sij) où sij=aij+bij pour tout i∈{1;2;…;n} et j∈{1;2;…;p}.
∘Produit d'une matrice par un réel
Pour tout réel k, le produit kA=(pij) est défini par pij=k,aij pour tout i∈{1;2;…;n} et j∈{1;2;…;p}.
Propriétés : Règles de calcul
Soient A, B et C trois matrices de même dimension n×p et soit k un nombre réel.
∘ L’addition est commutative : A+B=B+A.
∘ L’addition est associative : (A+B)+C=A+(B+C)=A+B+C.
∘ Le produit par un réel est distributif : k(A+B)=kA+kB.
∘ On note 0n,p la matrice nulle de dimension n×p dont tous les coefficients sont nuls.
On a : A+0n,p=A.
∘ kA=0n,p si, et seulement si, k=0 ou A=0n,p.
IV. Produit de matrices
Soit A=(aij) une matrice de dimension n×p et B=(bij) une matrice de dimension m×q.
Le produit matriciel AB est défini si, et seulement si p=m.
Alors AB=(pij) où, pour tous i∈1;2;…;n et j∈1;2;…;q,
pij=k=1∑paik,bkj
 Remarque : dans le produit AB, le nombre de colonnes de A doit être égal au nombre de lignes de B.
Remarque : dans le produit AB, le nombre de colonnes de A doit être égal au nombre de lignes de B.
Propriétés : Règles sur le produit de matrices
Soient A, B et C trois matrices, et soit k un nombre réel.
Les propriétés suivantes sont valables sous réserve que les calculs soient possibles.
∘ La multiplication est associative : (AB)C=A(BC)=ABC
∘ La multiplication est distributive : A(B+C)=AB+AC et (A+B)C=AC+BC
∘ (kA)B=A(kB)=k(AB)
∘ 0n,pA=A0n,p=0n,p
Remarque : le produit matriciel n’est pas commutatif. Il suffit de prendre un contre-exemple :
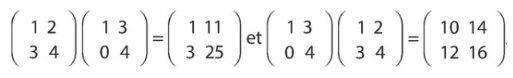




 est une matrice ligne
est une matrice ligne est une matrice colonne
est une matrice colonne est une matrice
est une matrice est une matrice diagonale
est une matrice diagonale