Une population évolue de manière linéaire si elle varie d’une quantité quasi-constante d’un palier au suivant.
Le modèle linéaire permet de rendre compte de cette évolution.
I. Le modèle linéaire en définitions
1) Qu’est-ce qu’une évolution linéaire ?
On considère une grandeur discrète, par exemple le nombre d’individus d’une population. Sa valeur initiale (au début de l’étude) est notée u0 ; n étant un entier naturel. On note ensuite un la valeur au palier n, c’est-à-dire après n unités de temps (années, mois, jours, etc.).
On dit que la grandeur varie de manière linéaire si et seulement si sa variation absolue un+1−un est constante, c’est-à-dire indépendante de la valeur de l’entier n.
Mots-clés
Une grandeur discrète est une grandeur mesurée à des paliers entiers, c’est-à-dire des intervalles de temps réguliers, et non de manière continue.La variation absolue est la différence des valeurs prises à deux paliers successifs.
La suite de terme général un est une suite arithmétique ; on passe d’un terme au suivant en ajoutant un nombre fixe r − la raison − positif ou négatif ; cette raison est la constante r=un+1−un.
On dit aussi que les nombres un sont en progression arithmétique.
Pour tout entier naturel n, on a : un=u0+n×r. Si f est la fonction telle que, pour tout entier naturel n, un=fn, alors f est une fonction affine.
2) Le sens de variation
Si r>0, la suite de terme général un est croissante.
La grandeur augmente au cours du temps.
Si r=0, la suite de terme général un est constante.
La grandeur est constante, elle ne varie pas au cours du temps.
Si r<0, la suite de terme général un est décroissante.
La grandeur diminue au cours du temps.
3) La représentation graphique
La représentation graphique de la suite, dans un repère R du plan, est l’ensemble des points de coordonnées n ; un.
Ces points appartiennent à la droite représentant la fonction f, ils sont donc alignés.
II. La modélisation de l’évolution d’une population
1) L’ajustement d’un nuage de points
Pour une grandeur dont la variation absolue est presque constante, c’est-à-dire ne connaît pas de différences importantes d’un palier au suivant, les points du nuage qui représente son évolution sont presque alignés.
On peut ajuster ce nuage par une droite.
Mais le modèle linéaire est inadapté pour des grandeurs dont la variation absolue change fortement d’un palier au suivant.
À noter
On « approxime » le nuage de points par une droite : on parle d’ajustement affine.
2) Les méthodes pour établir une droite d’ajustement
Il existe différentes méthodes pour déterminer une droite d’ajustement (dite aussi parfois « droite de tendance ») passant au plus près des points du nuage.
Les deux méthodes les plus utilisées sont les suivantes.
La méthode de Mayer (XVIIIe siècle) : les points du nuage sont partagés, par ordre d’abscisses croissantes, en deux sous-groupes de même effectif ; la droite de Mayer passe par les points moyens des deux sous-nuages ainsi définis.
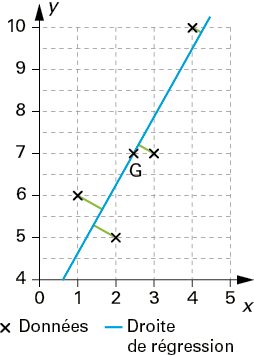
La méthode des moindres carrés, élaborée par Legendre et Gauss (XIXe siècle) ; on détermine la droite telle que la somme des carrés des distances de chaque point du nuage au point de la droite de même abscisse soit minimale. On montre que cette droite est unique et qu’elle passe par le point moyen du nuage ; on l’appelle droite de régression de y en x. Son équation peut être obtenue à l’aide d’une calculatrice ou d’un logiciel.
Zoom
La projection orthogonale sur une droite
On peut aussi déterminer la droite telle que la somme des carrés des distances des points du nuage à la droite soit minimale. On montre qu’une telle droite existe et est unique, et qu’elle passe par le point moyen G du nuage. On parle alors de régression orthogonale. En effet, la distance d’un point à une droite est la distance de ce point à son projeté orthogonal sur la droite.