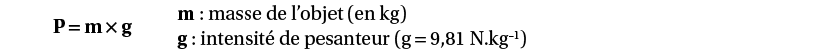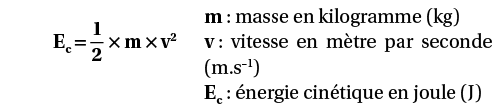Les forces
A) De l’action mécanique à la force qui la modélise
On appelle action mécanique tout phénomène susceptible de :
mettre en mouvement un objet ;
modifier le mouvement ou la trajectoire d’un objet ;
déformer un objet.
On distingue 2 types d’actions mécaniques :
s’il y a contact entre l’objet extérieur et l’objet étudié, on parle d’action mécanique de contact ;
s’il n’y a pas contact entre l’objet extérieur et l’objet étudié, on parle d’action mécanique à distance.
B) La notion de force
Une action mécanique exercée par un objet A sur un objet B peut être modélisée par une force : la force exercée par A sur B.
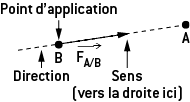
Les caractéristiques d’une force sont :
son point d’application (le point sur lequel elle s’exerce) ;
sa direction (ou droite d’action) ;
son sens (sens de son action sur sa droite d’action) ;
sa valeur (exprimée en Newton de symbole N).
Remarque
On représente une force par un vecteur contenant toutes les caractéristiques de la force qu’il représente. Ici, on l’écrit .
C) Les exemples de forces
a) Le poids
Tout corps à la surface de la Terre est soumis à l’attraction terrestre. La force exercée par la Terre sur un objet de masse m est appelée le poids.
Les caractéristiques du poids sont :
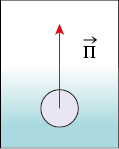
son point d’application : centre de gravité (centre d’inertie) de l’objet ;
Remarque
C’est une force à distance.
sa direction : verticale ;
son sens : vers le bas ;
sa valeur :
Exemple
En prenant g = 10 N.kg–1, la valeur du poids d’une personne de 80 kg est P = 80 × 10 = 800 N.
b) Les forces de frottement solide
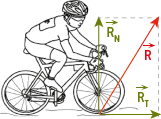
2 objets en contact exercent l’un sur l’autre des forces de frottement solide. La force exercée par un support sur un solide, notée , est une force répartie sur la surface de contact entre le solide et le support. Il est commode de décomposer la force R selon 2 composantes :
une composante normale dont la direction est perpendiculaire à la surface de contact (elle représente le fait que le solide ne passe pas à travers le support),
une composante tangentielle tangente à la surface de contact (elle représente les frottements entre le solide et le support).
La force est la somme vectorielle de ses 2 composantes : + .
Cas particulier : si les frottements sont négligés, alors = 0. Dans ce cas, .
Exemple
Les frottements de la roue de vélo sur le sol permettent au cycliste d’avancer. S’il n’y a pas de frottements, la roue glisse sur le sol.
c) La traînée
Un objet solide se déplaçant dans un fluide (l’eau, l’air…) subit une force de frottement fluide. Elle dépend du fluide, de la géométrie de l’objet, de sa vitesse par rapport au fluide et de la texture de la surface de l’objet. Cette force est parfois négligée.
Lorsqu’un objet se déplace à grande vitesse par rapport à un fluide de masse volumique ρfluide, il est soumis à une force de résistance aérodynamique appelée traînée, notée , dont les caractéristiques sont les suivantes :
son point d’application : un point de la surface de l’objet ;
sa direction : direction du mouvement de l’objet ;
son sens : dans le sens opposé à celui du mouvement de l’objet ;
sa valeur :
Remarque
CX dépend de la forme de l’objet et de la texture de sa surface ; il est mesuré en soufflerie. Il est de l’ordre de 0,01 pour une aile d’avion et varie entre 0,1 et 0,4 pour les automobiles.
DÉMONSTRATION
Une automobile se déplace à la vitesse de 130 km.h–1. Calculer la force de frottement due à l’air. À quelle vitesse cette automobile devrait-elle se déplacer pour réduire de moitié les frottements.
Données : masse volumique de l’air ρ =1,2 kg.m–3 ; pour cette automobile, Cx = 0,35 et S = 2,3 m2.
Réponse :
On calcule T après avoir converti la vitesse en m.s–1.
v = 130 km.h–1 = m.s–1 = 36,1 m.s–1, donc T = × 0,35 × 1,2 × 2,3 × 36,12 = 6,3 ×102 N.
On appelle T’ la valeur de la force de frottement réduite de moitié : T’ = .
Dans la formule de la trainée, seule la vitesse change. On la note v’.
Donc T’ = × CX × ρfluide × S × v2 = = × × CX × ρfluide × S × v2. Ainsi, après simplification, v’2 = v2.
Finalement, on obtient v’ = v = 26 m.s–1 = 92 km.h–1.
d) La poussée d’Archimède
Remarque
Les parties d, e et f concernent uniquement la filière STL.
La poussée d’Archimède est la force exercée par un fluide sur un objet placé au moins partiellement dans ce fluide. Elle est équivalente à l’ensemble des actions mécaniques agissant sur la partie immergée du solide.
Elle est modélisée par un vecteur :
direction : verticale ;
sens : vers le haut ;
norme ou valeur :
Elle s’applique au centre d’inertie du liquide déplacé, qui est en général le centre d’inertie du solide si celui-ci est totalement immergé.
e) La force d’interaction gravitationnelle
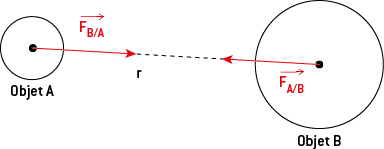
L’interaction gravitationnelle se manifeste entre les centres des deux corps A et B, de masses respectives mA et mB placés à une distance r = AB. Le corps A exerce sur le corps B une force gravitationnelle FA/B et le corps B exerce sur le corps A une force gravitationnelle FB/A. Ces deux forces ont la même direction, la même valeur mais sont de sens opposés, car ce sont des forces d’interaction.
Ces deux forces ont pour direction la droite AB. Elles sont uniquement attractives.
f) Les coordonnées de vecteurs sur des axes
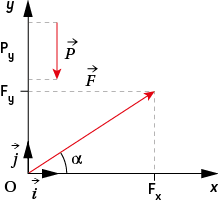
Les vecteurs disposent de coordonnées lorsqu’on utilise un repère. Ainsi le vecteur force poids, qui est vertical et dirigé vers le bas : son abscisse Px = 0 et son ordonnée Py = – P = – m × g car le vecteur est dirigé à l’envers du sens de l’axe (Oy).
Le vecteur poids a donc comme coordonnées (0, – mg).
Dans le cas général d’un vecteur incliné d’un angle α par rapport à l’axe (Ox) et de norme F, on détermine ses coordonnées par projections sur les axes en utilisant la trigonométrie : Fx = F × cos α et son ordonnée Fy = F × sin α.
Le vecteur force a donc comme coordonnées (F × cos α, F × sin α).
Les forces
A) De l’action mécanique à la force qui la modélise
On appelle action mécanique tout phénomène susceptible de :
mettre en mouvement un objet ;
modifier le mouvement ou la trajectoire d’un objet ;
déformer un objet.
On distingue 2 types d’actions mécaniques :
s’il y a contact entre l’objet extérieur et l’objet étudié, on parle d’action mécanique de contact ;
s’il n’y a pas contact entre l’objet extérieur et l’objet étudié, on parle d’action mécanique à distance.
B) La notion de force
Une action mécanique exercée par un objet A sur un objet B peut être modélisée par une force : la force exercée par A sur B.
Les caractéristiques d’une force sont :
son point d’application (le point sur lequel elle s’exerce) ;
sa direction (ou droite d’action) ;
son sens (sens de son action sur sa droite d’action) ;
sa valeur (exprimée en Newton de symbole N).
Remarque
On représente une force par un vecteur contenant toutes les caractéristiques de la force qu’il représente. Ici, on l’écrit .
C) Les exemples de forces
a) Le poids
Tout corps à la surface de la Terre est soumis à l’attraction terrestre. La force exercée par la Terre sur un objet de masse m est appelée le poids.
Les caractéristiques du poids sont :
son point d’application : centre de gravité (centre d’inertie) de l’objet ;
Remarque
C’est une force à distance.
sa direction : verticale ;
son sens : vers le bas ;
sa valeur :
Exemple
En prenant g = 10 N.kg–1, la valeur du poids d’une personne de 80 kg est P = 80 × 10 = 800 N.
b) Les forces de frottement solide
2 objets en contact exercent l’un sur l’autre des forces de frottement solide. La force exercée par un support sur un solide, notée , est une force répartie sur la surface de contact entre le solide et le support. Il est commode de décomposer la force R selon 2 composantes :
une composante normale dont la direction est perpendiculaire à la surface de contact (elle représente le fait que le solide ne passe pas à travers le support),
une composante tangentielle tangente à la surface de contact (elle représente les frottements entre le solide et le support).
La force est la somme vectorielle de ses 2 composantes : + .
Cas particulier : si les frottements sont négligés, alors = 0. Dans ce cas, .
Exemple
Les frottements de la roue de vélo sur le sol permettent au cycliste d’avancer. S’il n’y a pas de frottements, la roue glisse sur le sol.

c) La traînée
Un objet solide se déplaçant dans un fluide (l’eau, l’air…) subit une force de frottement fluide. Elle dépend du fluide, de la géométrie de l’objet, de sa vitesse par rapport au fluide et de la texture de la surface de l’objet. Cette force est parfois négligée.
Lorsqu’un objet se déplace à grande vitesse par rapport à un fluide de masse volumique ρfluide, il est soumis à une force de résistance aérodynamique appelée traînée, notée , dont les caractéristiques sont les suivantes :
son point d’application : un point de la surface de l’objet ;
sa direction : direction du mouvement de l’objet ;
son sens : dans le sens opposé à celui du mouvement de l’objet ;
sa valeur :
Remarque
CX dépend de la forme de l’objet et de la texture de sa surface ; il est mesuré en soufflerie. Il est de l’ordre de 0,01 pour une aile d’avion et varie entre 0,1 et 0,4 pour les automobiles.
DÉMONSTRATION
Une automobile se déplace à la vitesse de 130 km.h–1. Calculer la force de frottement due à l’air. À quelle vitesse cette automobile devrait-elle se déplacer pour réduire de moitié les frottements.
Données : masse volumique de l’air ρ =1,2 kg.m–3 ; pour cette automobile, Cx = 0,35 et S = 2,3 m2.
Réponse :
On calcule T après avoir converti la vitesse en m.s–1.
v = 130 km.h–1 = m.s–1 = 36,1 m.s–1, donc T = × 0,35 × 1,2 × 2,3 × 36,12 = 6,3 ×102 N.
On appelle T’ la valeur de la force de frottement réduite de moitié : T’ = .
Dans la formule de la trainée, seule la vitesse change. On la note v’.
Donc T’ = × CX × ρfluide × S × v2 = = × × CX × ρfluide × S × v2. Ainsi, après simplification, v’2 = v2.
Finalement, on obtient v’ = v = 26 m.s–1 = 92 km.h–1.
d) La poussée d’Archimède
Remarque
Les parties d, e et f concernent uniquement la filière STL.
La poussée d’Archimède
est la force exercée par un fluide sur un objet placé au moins partiellement dans ce fluide. Elle est équivalente à l’ensemble des actions mécaniques agissant sur la partie immergée du solide.
Elle est modélisée par un vecteur :
direction : verticale ;
sens : vers le haut ;
norme ou valeur :
Elle s’applique au centre d’inertie du liquide déplacé, qui est en général le centre d’inertie du solide si celui-ci est totalement immergé.
e) La force d’interaction gravitationnelle
L’interaction gravitationnelle se manifeste entre les centres des deux corps A et B, de masses respectives mA et mB placés à une distance r = AB. Le corps A exerce sur le corps B une force gravitationnelle FA/B et le corps B exerce sur le corps A une force gravitationnelle FB/A. Ces deux forces ont la même direction, la même valeur mais sont de sens opposés, car ce sont des forces d’interaction.
Ces deux forces ont pour direction la droite AB. Elles sont uniquement attractives.
f) Les coordonnées de vecteurs sur des axes
Les vecteurs disposent de coordonnées lorsqu’on utilise un repère. Ainsi le vecteur force poids, qui est vertical et dirigé vers le bas : son abscisse Px = 0 et son ordonnée Py = – P = – m × g car le vecteur est dirigé à l’envers du sens de l’axe (Oy).
Le vecteur poids a donc comme coordonnées (0, – mg).
Dans le cas général d’un vecteur incliné d’un angle α par rapport à l’axe (Ox) et de norme F, on détermine ses coordonnées par projections sur les axes en utilisant la trigonométrie : Fx = F × cos α et son ordonnée Fy = F × sin α.
Le vecteur force a donc comme coordonnées (F × cos α, F × sin α).
La deuxième loi de Newton
Remarque
Cette partie concerne uniquement la filière STL.
A) Énoncé
Dans un référentiel galiléen, la somme vectorielle des forces extérieures appliquées à un système est égale au produit de la masse de ce système par son vecteur accélération : Σ ext = m × .
B) Le cas d’une chute libre verticale
Lorsqu’un objet est en chute libre, il n’est soumis qu’à son poids = m × .
On considère une bille d’acier placée à une hauteur h = 1,0 m et lâchée sans vitesse initiale à t = 0. Cette bille est dense, elle ne subira que très peu les frottements de l’air et la poussée d’Archimède : elle est en chute libre.
On écrit alors la deuxième loi de Newton appliquée à la bille : Σext = m × , or Σ ext = = m × , ainsi m × = m × , donc l’accélération est égale au champ de pesanteur = .
Si on considère la chute de la bille sans vitesse initiale, elle est verticale, on n’utilise qu’un axe que l’on choisit orienté vers le haut. Le vecteur poids a une seule coordonnée Py = – m × g, donc le vecteur accélération a une seule coordonnée ay = – g.
On détermine alors le vecteur vitesse ayant une coordonnée vy(t) = – g × t + C, C étant une constante. Or à t = 0, v = 0, ainsi vy(0) = – g × 0 + C = C, ainsi la constante est nulle. Donc vy(t) = – g × t.
De même vy = , on obtient donc la position y(t) de la bille en intégrant la coordonnée du vecteur vitesse. y(t) = – × g × t2 + C′, C′ étant une constante. Or à t = 0, y = h, ainsi y(0) = – × g × 02 + C′ = C′, donc la constante vaut h = 2,0 m. Donc y(t) = – × g × t2 + h.
L’équation horaire de la position verticale est donc de la forme parabolique.
Il est possible de déterminer la date à laquelle la bille atteindra le sol, alors y(t) = 0, soit × g × t2 + h = 0, ainsi t2 = 2 × et t =.
Si on étudie l’évolution de la position de la bille à intervalle de temps constant (chronophotographie), on notera des points de plus en plus distants au cours du temps (fig. 1).
Dans le cas où des forces de frottements fluides interviennent, la vitesse augmente jusqu’à atteindre une valeur limite. Ceci se produit lorsqu’une bille est lâchée dans de l’huile : l’accélération de la bille diminue et le mouvement devient rectiligne et uniforme car les forces appliquées se compensent (fig. 2).
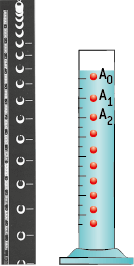
Fig. 1 Fig. 2
L'énergie cinétique dans un mouvement de translation
L’énergie cinétique d’un point matériel est l’énergie qu’il possède du fait de sa masse et de sa vitesse.
L’énergie cinétique Ec d’un point matériel de masse m, se déplaçant à la vitesse v, s’exprime par :
Dans un mouvement de translation, tous les points du solide ont la même vitesse v.
L’énergie cinétique du solide est donc la somme des énergies cinétiques des points matériels le constituant. La masse du solide est la somme de toutes les masses des points matériels. Ainsi, l’énergie cinétique du solide est : Ec = × m × v2 où m est la masse du solide.
La vitesse intervient au carré dans la formule énergie cinétique. Cela signifie que lorsque la vitesse est doublée, alors l’énergie cinétique est quadruplée.
Exemple
Un camion de masse m = 38 tonnes se déplace à vitesse constante v = 90 km.h–1 sur une route droite et horizontale. On recherche l’énergie cinétique de ce camion.
On peut employer la formule Ec = m × v2 pour calculer son énergie cinétique, puisque le camion a un mouvement de translation.
Il faut savoir que 1 m.s–1 = 3,6 km.h–1. Il faut convertir les valeurs numériques données pour pouvoir faire l’application numérique : m = 38 tonnes = 3,8 × 104 kg et v = 90 km.h–1 = 25 m.s–1.
Ainsi, l’énergie cinétique vaut Ec = 0,5 × 3,8 × 104 × 252 soit Ec = 1,2 × 107 J = 12 MJ.
Lorsque la variation d’énergie cinétique d’un système est positive alors sa vitesse augmente. Inversement si la variation d’énergie cinétique d’un système est négative alors sa vitesse diminue. Si la variation d’énergie cinétique d’un système est nulle, alors son mouvement est uniforme.
Le travail d'une force
A) Définition du travail
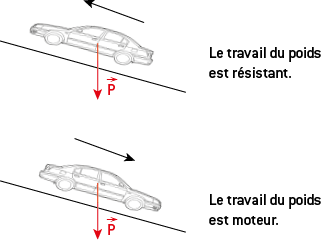
Le travail d’une force mesure l’effet de cette force sur le déplacement de son point d’application : si cette force contribue au déplacement de son point d’application, on dit que son travail est moteur et si cette force tend à s’opposer au déplacement de son point d’application, on dit que son travail est résistant.
B Le travail d’une force constante
Le travail WAB() d’une force constante , lorsque son point d’application se déplace d’un point A jusqu’à un point B, a pour expression :
Exemples
Calculer le travail de la force (F = 100 N) sur le chemin AB = 10 m.


C) La puissance moyenne
La puissance moyenne Pmoy d’une force pendant une durée Δt est le rapport du travail effectué W() par cette force sur la durée Δt :
La puissance moyenne pour modifier une vitesse pendant une durée donnée.
D) Le calcul d’une puissance moyenne
Si on veut faire évoluer la vitesse d’un système de masse m d’une valeur vA à une valeur vB au cours d’une durée Δt en l’absence de frottement, la puissance moyenne Pmoy s’exprime par :
Remarque
Les parties D et E concernent uniquement la filière STL.
Pmoy =
Exemple
Si on veut que la vitesse d’une moto de masse m = 350 kg (avec le motard) passe de vA = 10 m.s–1 à vB = 25 m.s–1 en une durée ∆t = 2,0 s, il faut fournir une puissance mécanique moyenne Pmoy = = = = 46 kW.
Si on veut maintenir la vitesse d’un système de masse m à une valeur v au cours d’une durée Δt en présence d’une force de frottement f, la puissance moyenne Pmoy s’exprime par : Pmoy = – = × car il faut compenser la puissance dissipée par la force de frottement. Si la force de frottement est dans le sens opposé au vecteur vitesse alors Pmoy = – f × v.
Exemple
Si on veut que la vitesse d’une moto de masse m = 350 kg (avec le motard) conserve sa valeur v = 25 m.s–1 avec une force frottement de norme f = 500 N opposée à la vitesse, il faut fournir une puissance mécanique moyenne Pmoy = f × v = 500 × 25 = 13 kW.
E) Le théorème de l’énergie cinétique
On appelle théorème de l’énergie cinétique la relation entre la variation d’énergie cinétique et le travail des forces. Dans un référentiel galiléen, la variation d’énergie cinétique d’un solide de masse m en translation entre deux positions A et B, est égale à la somme des travaux des forces extérieures appliquées au solide entre les positions A et B :
ΔEcA→B = EcB – EcA = Σ W(ext)A→B = m × v2B × m × v2A
où vA et vB sont les vitesses instantanées du solide aux positions A et B.
Le transfert d'énergie par travail mécanique
A) Les énergies potentielles
Remarque
Cette partie concerne uniquement la filière STI2D.
a) L’énergie potentielle de pesanteur Epp
L’énergie potentielle de pesanteur Epp résulte de l’interaction gravitationnelle entre le solide et la Terre. Cette énergie est liée à sa position par rapport à la Terre.
L’énergie potentielle de pesanteur est notée Epp. Un solide de masse m, placé à une hauteur h par rapport à une référence, a une énergie potentielle de pesanteur :
Remarque
h, la hauteur, dépend de la référence fixée.
Exemple
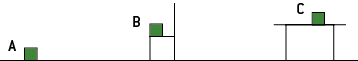
Un cube de petite taille, de masse m = 10 kg, est placé en 3 endroits différents : en A, au niveau du sol ; en B, sur une chaise ; en C sur une table.
Le champ de pesanteur est uniforme et a une norme g = 10 N.kg–1.
Déterminez la hauteur du cube dans les 3 cas, si on considère que le sol est la référence de hauteur h = 0, puis l’énergie potentielle de pesanteur du cube dans les 3 cas.
L’assise de la chaise est à 0,50 m du sol et le dessus de la table à 0,80 m.
L’altitude du centre d’inertie correspond à la hauteur où il est placé car la référence est le sol, donc :
en A : hA = 0 m soit EppA = m × g × hA ainsi EppA = 10 × 10 × 0 = 0 J ;
en B : hB = 0,50 m soit EppB = m × g × hB ainsi EppB = 10 × 10 × 0,50 = 50 J ;
en C : hC = 0,80 m soit EppC = m × g × hC ainsi EppC = 10 × 10 × 0,80 = 80 J.
b) L’énergie potentielle élastique Epe
Un ressort comporte des spires. Lorsqu’il est au repos, il a une longueur à vide l0.
Il peut être étiré ou comprimé, il revient vers sa position de repos lorsqu’il est lâché. Ainsi, un ressort dispose d’énergie lorsqu’il n’est pas dans sa position de repos.
Certains ressorts sont plus difficiles que d’autres à étirer ou à comprimer car ils ont une constante de raideur k plus élevée. La constante de raideur k d’un ressort s’exprime en newton par mètre (N.m–1). Elle donne une information concernant la valeur de la force à exercer sur un ressort pour pouvoir l’étirer ou le comprimer d’une certaine longueur.
On note ∆l = l – l0 l’allongement du ressort, où l est la longueur du ressort. Si le ressort est étiré, l’allongement est positif. Si le ressort est comprimé, l’allongement est négatif.
L’énergie potentielle élastique se note Epe. Elle s’exprime par :
k : constante de raideur du ressort en newton par mètre (N.m–1)
Epe = × k × ∆l2 ∆l : allongement en mètre (m)
Epe : énergie potentielle élastique en joule (J)
B) L’énergie mécanique
a) Définition
L’énergie mécanique d’un solide est la somme de son énergie cinétique (de translation et de rotation) et de son énergie potentielle (de pesanteur et élastique) :
Em = Ec + Ep Em : énergie mécanique qui s’exprime en joule (J)
b) La conservation de l’énergie mécanique
Lorsque l’on frappe un ballon vers le haut, il a une trajectoire en cloche.
On considère un ballon de masse m = 450 g partant depuis un point O avec une vitesse initiale v0 = 15 m.s–1. Le point O est pris comme la référence de l’énergie potentielle, c’est-à-dire que O a une altitude nulle. Le mouvement du ballon est dans l’air sans frottement.
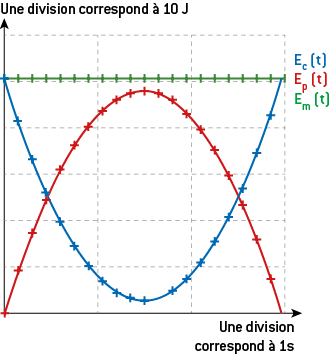
On peut filmer le mouvement du ballon et déterminer l’énergie cinétique, l’énergie potentielle et l’énergie mécanique en différentes positions de la trajectoire. On obtient un ensemble de courbes d’énergies en fonction du temps.
Lorsque le ballon monte, son énergie cinétique diminue. Il ralentit et son énergie potentielle de pesanteur augmente. De l’énergie cinétique est donc transformée en énergie potentielle de pesanteur.
Cet échange se réalise dans l’autre sens lors de la descente. L’énergie potentielle de pesanteur diminue car l’altitude du ballon diminue et en même temps, la vitesse du ballon augmente ainsi que son énergie cinétique.
La variation d’énergie cinétique est l’opposé de la variation d’énergie potentielle de pesanteur puisque l’énergie mécanique, qui est la somme des 2, reste constante.
Il y a conservation de l’énergie mécanique du ballon au cours de ce mouvement : il n’y a pas de transformation d’énergie mécanique sous forme d’énergie interne ou de transfert thermique, c’est pour cela que l’énergie mécanique se conserve.
c) La non-conservation de l’énergie mécanique
L’énergie mécanique d’un solide ne se conserve pas en général, à cause de frottements. Il y a alors augmentation de l’énergie interne du solide, qui se traduit par une élévation de sa température ou un transfert thermique vers le milieu extérieur.
L’énergie mécanique diminue alors, ce qui entraîne une diminution de l’énergie cinétique et ou de l’énergie potentielle du solide.
Exemples
On accroche une masse à un fil fixé à un support, puis on écarte le fil et la masse de leur position de repos : l’ensemble décrit des arcs de cercle périodiques, mais l’amplitude des va-et-vient diminue, ce qui traduit une diminution de l’énergie mécanique.
On retourne une bicyclette et on fait tourner la roue avant. La vitesse de rotation de la roue diminue progressivement jusqu’à s’arrêter. L’énergie mécanique de la roue après la mise en rotation n’est pas conservée, l’énergie cinétique finit par s’annuler.
Lorsqu’une force de frottement est présente, l’énergie mécanique du système peut diminuer sauf si elle est compensée par un apport d’énergie pour relancer le système.