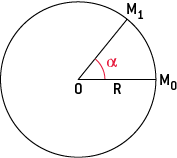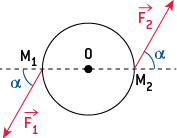Légende de la leçon
Vert : définitions
I. La deuxième loi de Newton
1) Énoncé
Dans un référentiel galiléen, la somme vectorielle des forces extérieures appliquées à un système est égale au produit de la masse de ce système par son vecteur accélération :
Σ F→ext = m × a→.
2) Détermination de l’accélération pour une chute libre
Lorsqu’un objet est en chute libre, il n’est soumis qu’à son poids :
P→ = m × g→, où g→ est l’accélération de la pesanteur.
C’est le cas pour une bille d’acier placée à une hauteur h = 1,0 m et lâchée sans vitesse initiale à t = 0. Cette bille est dense, elle ne subira que très peu les frottements de l’air et la poussée d’Archimède.
On écrit alors la deuxième loi de Newton appliquée à la bille : Σ F→ext = m × a→, or Σ F→ext = P→ = m × g→, ainsi m × a→ = m × g→. L’accélération est donc égale au champ de pesanteur : a→ = g→.
La bille adopte alors un mouvement vertical vers le bas uniformément accéléré.
3) Détermination de la résultante des forces à partir du vecteur accélération
Une vidéo peut être analysée en pointant les positions successives occupées par un point d’un solide. On obtient ainsi la trajectoire de ce point. Ainsi, la position du centre d’inertie d’un parachutiste a été trouvée de cette manière et figure sur le schéma à droite. La durée entre deux images ou deux positions successives est 30 ms. On obtient alors l’évolution de la vitesse et de l’accélération au cours du temps.
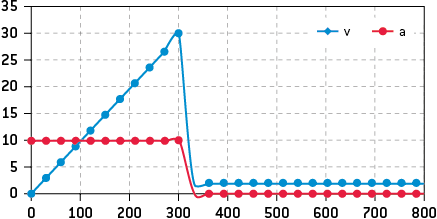
Un logiciel permet alors la détermination des coordonnées en indiquant un étalon de distance, ce qui conduit à trouver les coordonnées du vecteur vitesse et ensuite celles du vecteur accélération. On construit alors le graphe ci-dessous représentant l’évolution des valeurs de la vitesse et de l’accélération au cours du temps.
Il y a deux phases :
- une phase de chute libre verticale avec une accélération constante a = 10 m.s–2 et une résultante des forces égale au poids de l’ensemble parachute et parachutiste ;
- une seconde phase avec un mouvement vertical et une accélération nulle. La résultante des forces est donc nulle, la force de frottement liée au parachute ouvert compense le poids de l’ensemble parachute et parachutiste.
II. Les forces de frottement
1) Théorème de l’énergie cinétique
Rappel : le théorème de l’énergie cinétique établit la relation entre la variation d’énergie cinétique et le travail des forces. Dans un référentiel galiléen, la variation d’énergie cinétique d’un solide de masse m en translation entre deux positions A et B est égale à la somme des travaux des forces extérieures appliquées au solide entre les positions A et B :
ΔEcA→B = EcB – EcA = Σ W(F→ext)A→B = 12 mv2B × 12 mv2A où vA et vB sont les vitesses instantanées du solide aux positions A et B.
En général, le travail d’une force de frottement est résistant.
2) Cas d’une force de frottement entre un solide et un fluide
La force de frottement entre un solide et un fluide est liée à la vitesse : sa valeur peut être proportionnelle à la valeur de la vitesse (f = k × v) ou au carré de la vitesse (f = k × v2). Le travail d’une force de frottement f→ est résistant.
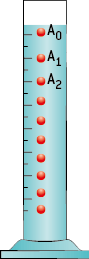
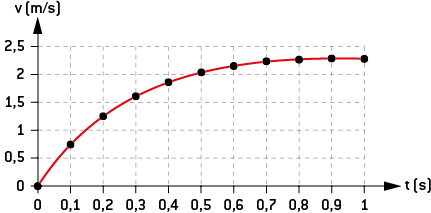
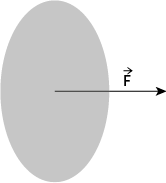
Un solide lâché sans vitesse initiale dans un fluide moins dense que lui accélère de moins en moins vite jusqu’à ce que sa vitesse soit constante (voir le schéma ci-contre).
La vitesse augmente donc et se stabilise comme sur le graphe page suivante.
3) Cas d’une force de frottement entre solides
Le travail d’une force de frottement constante f→ sur un déplacement rectiligne de longueur AB vaut W(f→)A→B = – f × AB.
Pour déterminer la valeur f de la force de frottement constante f→, on détermine la longueur AB du parcours horizontal d’un solide ayant une vitesse initiale vA avant de s’arrêter.
Les travaux de la force poids P→ et de la réaction normale R→N sont nuls, aussi la variation d’énergie cinétique est égale au travail de la force de frottement : ΔEcA→B = EcB – EcA = W(f→)A→B = –f × l, donc 12 mvB2 – 12 mvA2 = – f × AB.
Or le solide stoppe en B, ainsi vB2 = 0, donc – 12 mvA2 = – f × AB, soit 12 mvA2 = f × AB ou f = m×vA22×AB.
La valeur f est inversement proportionnelle à la distance d’arrêt.
III. Les mouvements de rotation
1) La relation entre les vitesses angulaire ω et linéaire v
Lors d’une rotation, un point mobile M de l’objet décrit un arc de cercle centré sur l’axe de rotation passant par O pendant une durée Δt. La vitesse angulaire ω est le quotient de l’angle α balayé par la durée Δt mise pour effectuer cette rotation.
Le point M parcourt alors le cercle avec une vitesse v liée à la vitesse angulaire ω et au rayon R :
2) Le moment d’une force
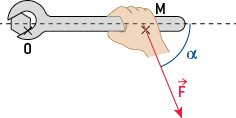
Le moment M d’une force de valeur F par rapport à un point O mesure la capacité pour cette force de faire tourner un système autour du point O. Soit M le point d’application de F→ et α l’angle entre OM→ et F→. La valeur de M est donnée par :
Le moment est une grandeur algébrique. Après avoir défini un sens positif de la rotation, il faut déterminer le signe du moment. Si la force contribue à la rotation du système dans le sens positif, son moment est positif. Dans le cas contraire, il est négatif.
Exemple
Une main exerce une force F→ de valeur F = 100 N faisant un angle α = 70° par rapport à la clé. Le point d’application de F, noté M, se trouve à une distance de 22 cm du centre de l’écrou, noté O. Le moment de cette force par rapport au centre de l’écrou vaut :
M = F × OM × sinα = 100 × 0,22 × sin70 = 21 N.m.
3) Le moment d’un couple de forces
Un couple de forces est l’ensemble formé par deux forces F1 et F2 telles que :
F→1 + F→2 = 0→ ;
F→1 et F→2 ont des droites d’action différentes.
La valeur du moment M d’un couple de forces F→1 et F→2, dont les points d’application M1 et M2 sont alignés avec le point O autour duquel l’objet est en rotation, est donnée par :
On définit un sens positif de la rotation. Si le couple de forces contribue à la rotation du système dans le sens positif, son moment est positif. Dans le cas contraire, il est négatif.
IV. Les fluides incompressibles
1) Définitions
Un fluide est un milieu matériel déformable qui n’a pas de forme propre, c’est-à-dire qu’il épouse la forme de son contenant. Ce peut être un liquide ou un gaz. On dit qu’un fluide est parfait lorsque sa viscosité est nulle et qu’il ne conduit pas la chaleur.
Un fluide incompressible ne peut être ni comprimé ni dilaté. Sa masse volumique est donc constante : elle ne dépend pas de la température ni de la pression. Les liquides sont considérés comme des fluides incompressibles, contrairement aux gaz.
2) La pression et la force pressante
Une force pressante est représentée par un vecteur force F→ agissant uniformément et perpendiculairement sur la surface S. Elle exerce alors une pression P sur la surface S. La pression P s’exprime par :
Remarques
La pression de l’air ambiant est la pression atmosphérique, elle a une valeur voisine de 105 Pa. Une pression égale à 1 pascal est une toute petite pression. 1 Pa = 1 N.m–2.
On emploie aussi fréquemment comme unité de pression :
- l’hectopascal : 1 hPa = 1 × 102 Pa ;
- le bar : 1 bar = 1 × 105 Pa ;
- l’atmosphère : 1 atm = 1,013 × 105 Pa ;
- le centimètre de mercure : 1 cm Hg = 1,3 kPa.
Application
Une force pressante F→, dont la valeur est F = 500 N, s’exerce perpendiculairement à une paroi d’aire S = 50 cm2. Calculer alors la pression exercée par cette force sur cette surface.
On convertit l’aire en mètre carré : S = 50 × 10–4 m2.
La pression se calcule selon P = FS soit P = 50050 x 10−4 = 1,0 × 105 Pa.
3) La pression absolue, relative ou différentielle
On mesure la pression dans un fluide avec un manomètre. Pour mesurer la pression atmosphérique, on utilise un baromètre. Il existe trois types de pressions mesurées :
- la pression absolue dans un fluide : c’est la pression dans ce fluide par rapport à la pression dans le vide (dans le vide, la pression est nulle) ;
- la pression relative dans un fluide : c’est la pression dans ce fluide par rapport à la pression atmosphérique (Prelative = Pabsolue – Patmosphérique) ;
- une pression différentielle : c’est la différence entre deux pressions, la seconde pouvant servir de pression de référence.
Application
La pression relative mesurée dans une conduite de gaz est de 1,55 bar. En déduire la pression absolue correspondant à cette pression relative (écrire le résultat en bars). Convertir cette pression en pascals, puis en hectopascals.
Donnée : la pression atmosphérique autour de la conduite est de 1,01 bar.
On utilise la relation Pabsolue = Prelative + Patmosphérique = 1,55 + 1,01 = 2,56 bar.
Or 1 bar = 105 Pa et 1 hPa = 1 × 102 Pa, ainsi Prelative = 2,56 × 105 Pa = 2,56 × 103 hPa.
4) Le principe fondamental de l’hydrostatique
On considère un fluide incompressible de masse volumique ρ, à l’équilibre dans le référentiel terrestre (c’est-à-dire qu’il est immobile par rapport au référentiel terrestre). Ce fluide n’étant soumis qu’à la pesanteur terrestre, la différence de pression ΔP entre deux points A et B situés à des profondeurs hA et hB est donnée par la relation :
Remarques
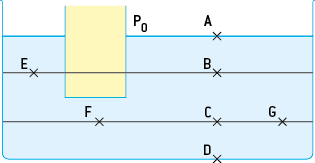
Un réservoir en U est schématisé ci-contre. Il contient un fluide en contact avec une pression P0. Comparons les pressions en A, B, C, D, E, F et G.
Plus la profondeur augmente, plus la pression augmente (PA < PB < PC < PD).
Deux points situés à la même profondeur sont à la même pression (PB = PE, PF = PC = PG).
Il y a continuité de la pression à l’interface entre deux fluides (PA = P0).