Les informations délivrées par les médias sont truffées de nombres : pourcentages, pourcentages de pourcentages, indices, coefficients multiplicateur, variations absolues, relatives... Comment s’y retrouver ?
I Pourcentages
1 Généralités
Un pourcentage est une façon particulière d’écrire une fraction : au lieu d’écrire (a sur 100 ou a centièmes) on écrit a % (a pour cent).
Pour calculer un pourcentage d’une quantité, on en calcule une fraction dont le dénominateur est 100.
Exemple : Dans un lycée de 200 élèves il y a 48 latinistes. La proportion, ou fraction,
de latinistes est . Il y a donc 24 % de latinistes.
« Appliquer un pourcentage (ou un taux de pourcentage) » d’une quantité est synonyme de « multiplier la quantité par la fraction correspondante ».
Exemple : 32 % de 190 valent.
2 Coefficients multiplicateurs
Repère
À noterLorsqu’une quantité q augmente de t %, puis diminue de t %, la quantité obtenue n’est pas égale à q.
Si on augmente une quantité q de t % on obtient la quantité :
En effet, si q augmente de t %, alors elle se transforme en une quantité q′ égale à q
à laquelle on ajoute l’augmentation qui vaut .
Si on diminue une quantité q de t % on obtient la quantité :
En effet, si q diminue de t %, on soustrait q × t % à la quantité initiale.
II Variations absolues et variations relatives
Lorsqu’une quantité varie de la valeur initiale vi à la valeur finale vf :
• sa variation absolue est la différence vf – vi ;
• sa variation relative (ou taux d’évolution) est le quotient . Elle mesure
la fraction que représente la variation absolue par rapport à la valeur initiale. Elle s’exprime généralement en pourcentage.
Méthode
Augmentations et réductions
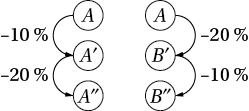
Première étape. On dispose d’une somme A. On enlève 10 % de sa valeur, on obtient A′. On enlève à cette somme A′ 20 % de sa valeur, on obtient A″.
Deuxième étape. Reprenons cette même somme A. On lui enlève 20 % de sa valeur ce qui donne B′ On enlève à B′ 10 % de sa valeur, on obtient B″.
1. L’une des deux sommes A″ ou B″ représentent-elles 70 % de la somme initiale A ?
2. A-t-on A″ = B″ ? Justifier la réponse.
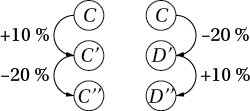
3. La réponse à la question 2. reste-t-elle valable pour la situation décrite par le schéma ci-contre ?
Repère
Conseils1. On peut répondre facilement en prenant un exemple simple.
2. et 3. La façon la plus efficace de répondre consiste à utiliser les coefficients multiplicateurs.
Solution
À noter
Les pourcentages de baisse ne s’ajoutent pas.
1.Si A = 100 on trouve successivement et A′ = 90 × 0,8 = 72. Donc A″ n’est pas égale à 70 % de A mais à 72 % de A.
De même B″ n’est pas égale à 70 % de A.
2. et .
et .
DoncA″ =B″. Ces sommes représentent toutes les deux 72 % de A, c’est-à-dire A diminuée de 28 % de sa valeur.
3. et
.
et .
DoncC″ =D″. Elles représentent toutes les deux 88 % de C.