Géométrie du cercle, du triangle, de la sphère ; aires et volumes

Ce fichier regroupe ce qui doit être bien maîtrisé des programmes des classes antérieures concernant : 

I. Géométrie du cercle 

II. Droites parallèles et droites perpendiculaires,angles alternes internes et angles correspondants

III. Géométrie du triangle

IV. Perspective cavalière

V. Géométrie de la sphère

VI. Aires

VII. Volumes

I. Géométrie du cercle 

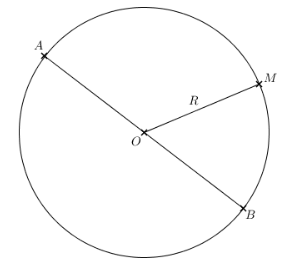
Définition : Un cercle de centre $O$ et de rayon $R$ est l'ensemble des points $M$ du plan situé à la distance $R$ de $O$.
Remarque : Tous les points du cercle vérifie alors $OM=R$.

Définition :

• On dit que $OM$ est un rayon du cercle.

•  Si deux points $A$ et $B$ d'un cercle sont tels que le centre $O$ appartient au segment $[AB]$, on dit que $[AB]$ est un diamètre du cercle et que les points $A$ et $B$ sont diamétralement opposés.

Propriété :
On considère deux points $A$ et $B$ d'un cercle de centre $O$ et de rayon $R$ tels que $[AB]$ soit un diamètre de ce cercle.
On a alors :

• $O$ est le milieu de $[AB]$

• $AB=2\times R$

• Le périmètre du cercle est $\mathscr{P}=2\times \pi \times R$

• L'aire d'un disque est $\mathcal{A}=\pi \times R \times R = \pi\times R^2$

Exemple : Si un cercle a un rayon de $3$ cm alors son diamètre est de $2\times 3=6$ cm, son périmètre est de $\mathscr{P}=6\times \pi$ cm. L'aire du disque correspondant est $\mathcal A=9\times \pi$ cm² .

II. Droites parallèles et droites perpendiculaires, angles alternes internes et angles correspondants

Notation : $(d)$ parallèle à $(d')$ se note $(d)~\parallel ~(d')$ 

ou si elles sont confondues : 

Tracé à la main :

Propriétés : 

• Si deux droites sont parallèles à une même troisième alors elles sont parallèles entre elles.

•  Si deux droites sont perpendiculaires à une même troisième alors elles sont parallèles entre elles.

•  Si deux droites sont parallèles, toute perpendiculaire à l'une est perpendiculaire à l'autre.

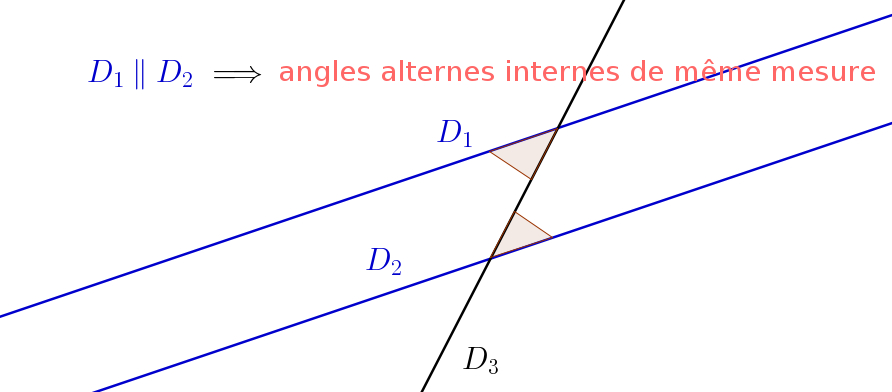
Angles alternes-internes : 

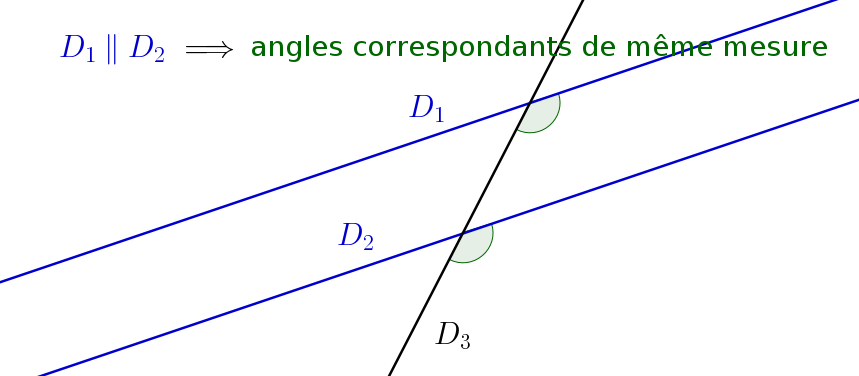
 Angles correspondants : 

III. Géométrie du triangle

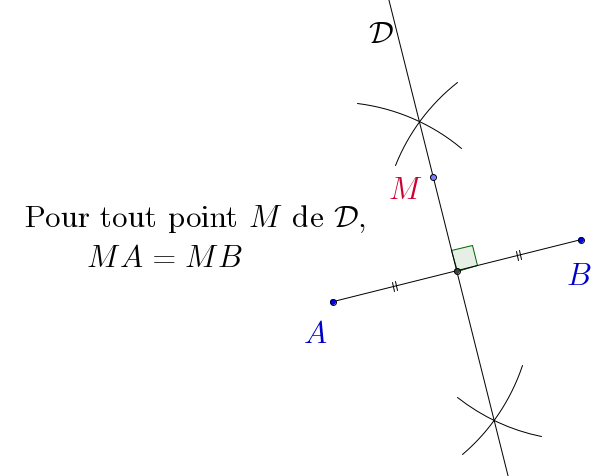
Rappel : Médiatrice d'un segment

Droite perpendiculaire au segment en son milieu.

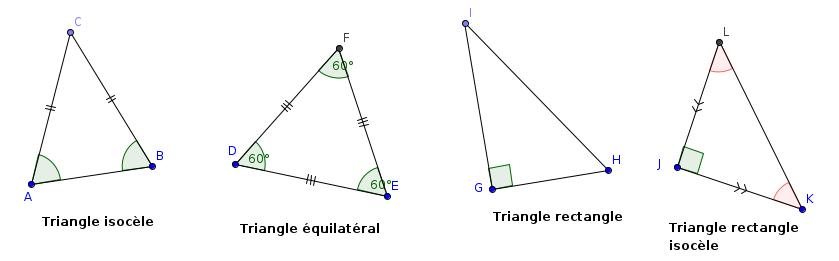
Triangles particuliers : 

(tenir le téléphone au format paysage pour éviter les déformations des figures)

La somme des angles d'un triangle vaut toujours 180° 180 degrés) ou $\pi$ rad $\pi$ radians).

Droites particulières dans un triangle : 

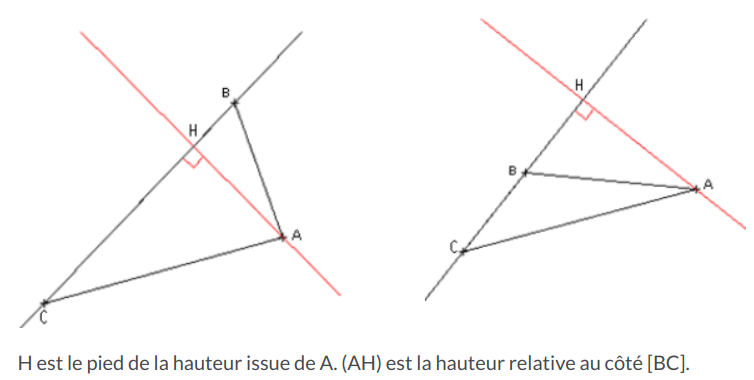
Hauteurs :

(si on peut, tenir le téléphone au format paysage pour éviter les déformations des figures)

Dans un triangle, les trois hauteurs sont concourantes en l'orthocentre du triangle.

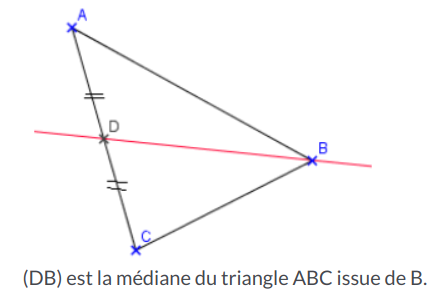
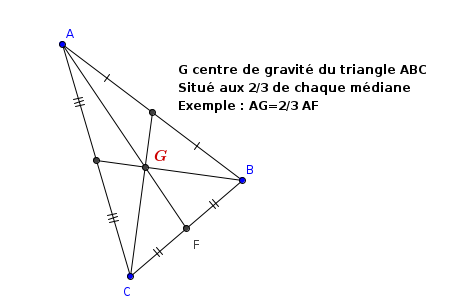
Médianes : 

Dans un triangle, les trois médianes sont concourantes au centre de gravité du triangle.

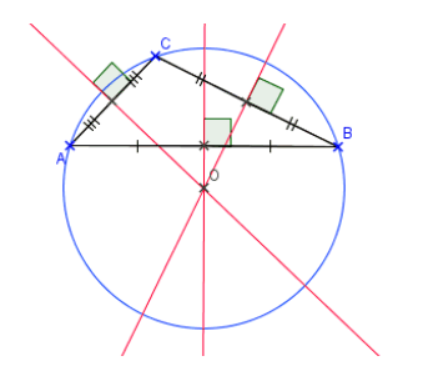
Médiatrices :

Dans un triangle, les trois médiatrices sont concourantes. Le point commun à ces trois médiatrices est le centre du cercle passant par les trois sommets du triangle.

Ce cercle est appelé le cercle circonscrit au triangle.

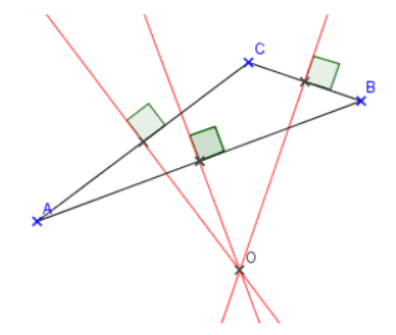
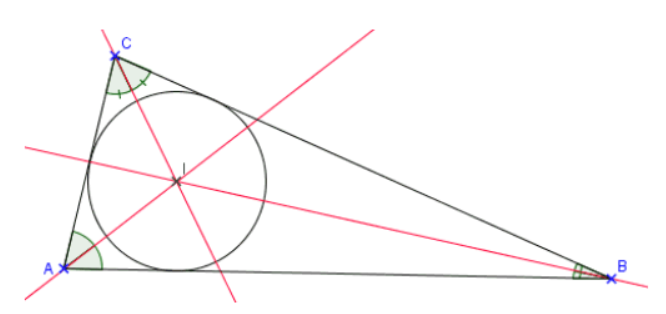
Bissectrices : 

(tenir le téléphone au format paysage pour éviter les déformations des figures)

La bissectrice d'un angle est la droite qui passe par le sommet et qui partage l'angle en deux angles de même mesure. Les trois bissectrices d'un triangle sont concourantes. 

Le point de concours des trois bissectrices d'un triangle est le centre du cercle inscrit du triangle.

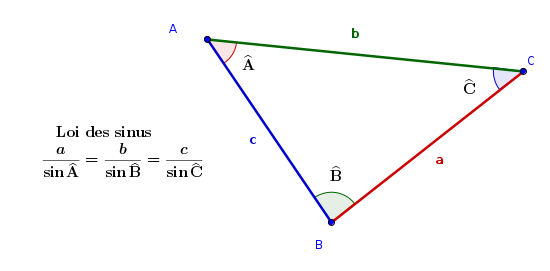
Loi des sinus et principe de triangulation (qui sera peut-être présenté au cours de cette année et qui permet d'évaluer des distances sur la surface de la terre par exemple) repose sur la loi des sinus (non vue dans les classes antérieures)

Le modèle utilisé dans la triangulation assimile des arcs de cercles à des segments. 

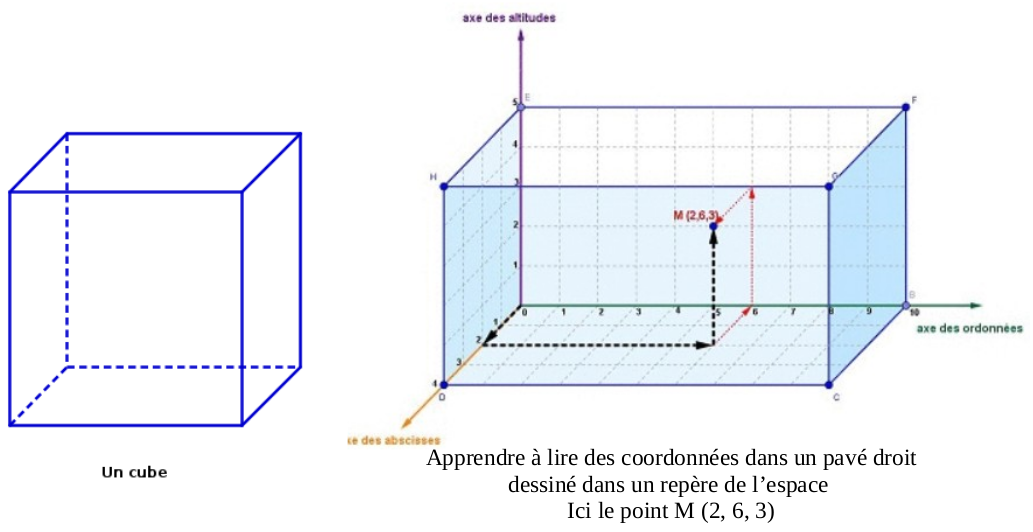
IV. Perspective cavalière

Technique de représentation, sur un support en deux dimensions, d'objets qui existent en volume (trois dimensions)

(tenir le téléphone au format paysage pour éviter les déformations des figures)

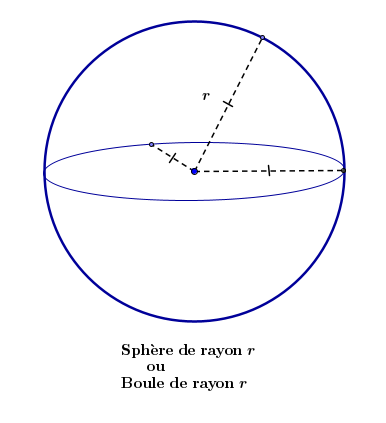
La sphère est creuse, la boule est pleine.

V. Géométrie de la sphère

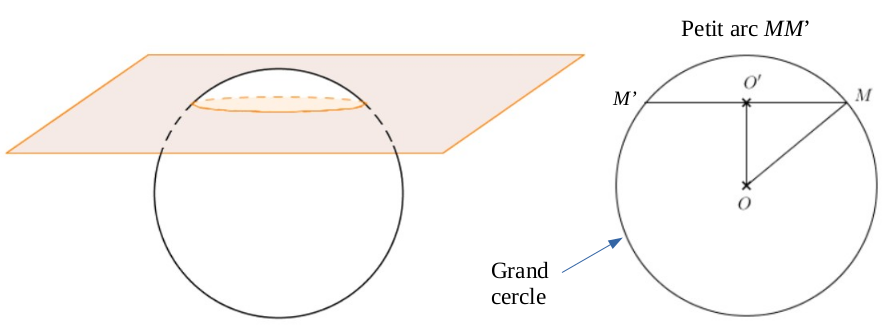
La section d'une sphère par un plan est un cercle.

(tenir le téléphone au format paysage pour éviter les déformations des figures)

Si on appelle $O'$ le centre du cercle de section et $O$ le centre de la sphère, alors la droite $(OO')$ est perpendiculaire au plan de section.
Le point $M$ étant un point de la sphère, la distance $OM$ est égale au rayon du cercle. On peut ainsi appliquer le théorème de Pythagore dans le triangle $OO'M$ si on connaît une deuxième longueur pour calculer la longueur manquante.

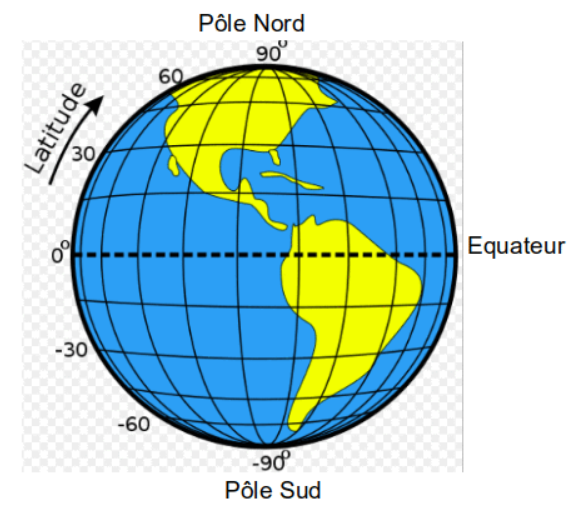
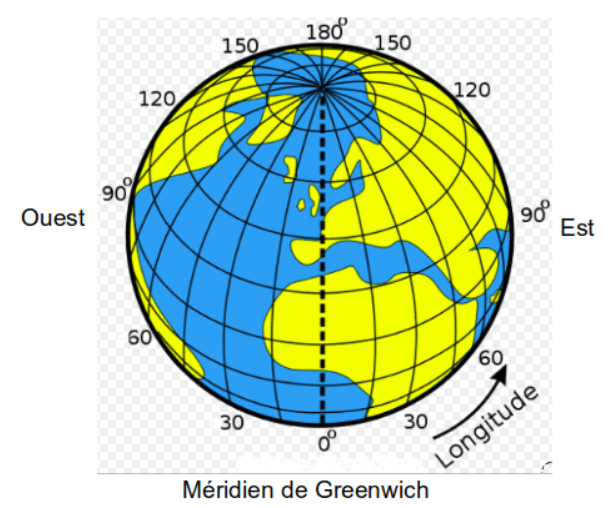
En géographie, on repère les points sur le globe terrestre à l'aide de parallèles et de méridiens.

La terre est assimilée à une sphère.

Pour se repérer sur la terre, l'homme y trace des lignes imaginaires.

Il trace tout d'abord l'équateur (en pointillé sur le dessin ci-après), ainsi que des parallèles à cet équateur. On en crée 90 dans l'hémisphère nord et 90 dans l'hémisphère sud.
Cela va permettre de repérer dans un premier temps la latitude de tout point de la terre.

Les parallèles sont des cercles parallèles à l'équateur ; ils sont numérotés de 0° à 90° vers le nord, et de 0° à 90° vers le sud. Cette numérotation permet de calculer la latitude (nord ou sud)

Dans un deuxième temps, on choisit un repère "vertical" le méridien de Greenwich en pointillé sur le dessin ci-dessous. Puis sont dessinés les méridiens parallèles au méridien de Greenwich,

Les méridiens sont des demi-cercles qui joignent les deux pôles ; ils sont numérotés de : 0° à 180° vers l'est et de 0° à 180° vers l'ouest. Cette numérotation permet de calculer la longitude (est ou ouest)

Quand on croise les parallèles et les méridiens on obtient un quadrillage qui permet de se repérer : La Terre ainsi quadrillée, on peut y situer tout point en donnant d'abord sa latitude (nord ou sud) puis sa longitude (est ou ouest).

On admet que le plus court chemin entre deux points de la terre est la longueur du plus petit arc du grand cercle qui les relie (sur la figure ci-dessus, il s'agit du petit arc $MM'$). Cette distance est appelée géodésique.

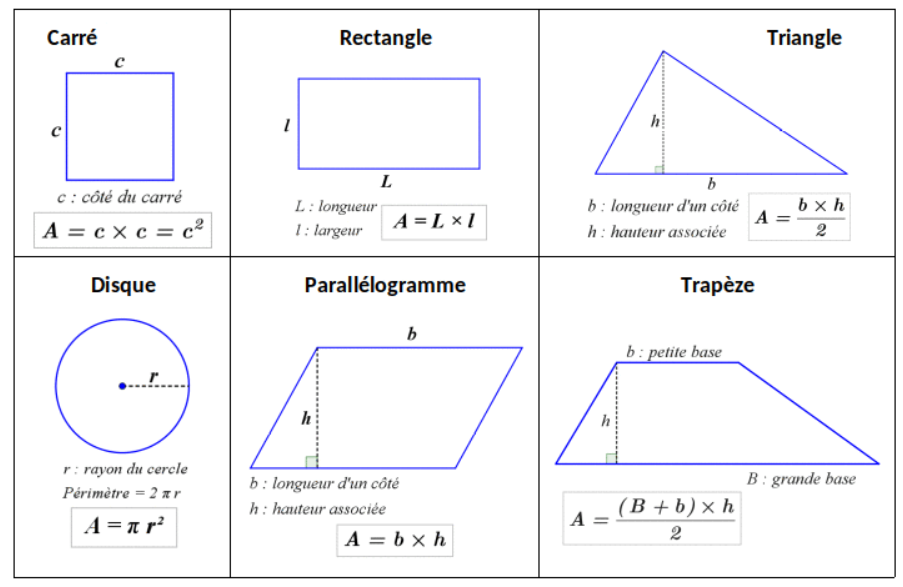
VI. Aires

(tenir le téléphone au format paysage pour éviter les déformations des figures)

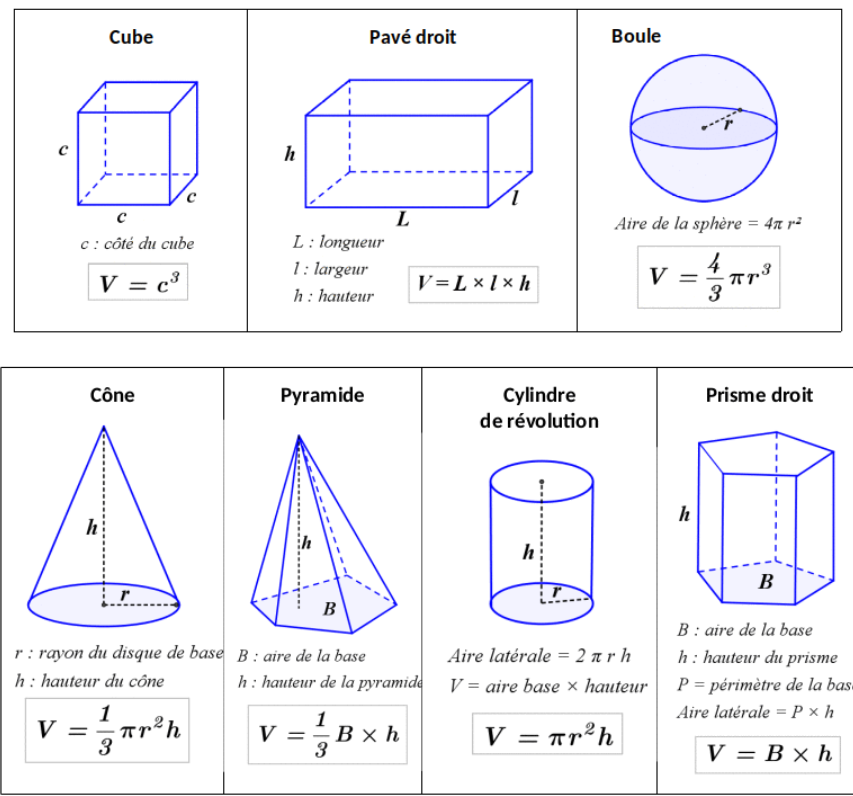
VII. Volumes

(tenir le téléphone au format paysage pour éviter les déformations des figures)