Fonctions affines

Les fonctions affines sont les plus simples à étudier. Le cas particulier des fonctions linéaires modélise la proportionnalité de deux grandeurs.

Repère
Mots clés

Dans le cas où a = 0, f est constante. Dans le cas où b = 0, f est linéaire.

I Caractéristiques des fonctions affines

Étant donnés deux réels a et b, dire qu’une fonction f est affine signifie que, pour tout x, on a :

f(x) = ax + b

Tableau de variation

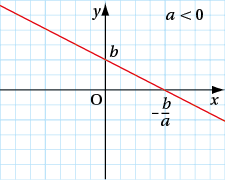
Représentation graphique

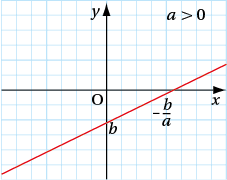
La représentation graphique d’une fonction affine est une droite.

a s’appelle le coefficient directeur de f et b s’appelle l’ordonnée à l’origine.

Repère
À noter

La droite passe par l’origine du repère si et seulement si b = 0. Elle est « horizontale » si et seulement si a = 0.

II Détermination d’une fonction affine

On peut déterminer une fonction affine f :

• à l’aide des coordonnées de deux points de sa représentation graphique.

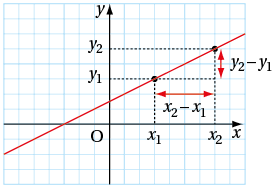
Exemple : Ci-contre, on a y1 = f(x1) et y2 = f(x2). Si on connaît les points (x1 ; y1) et (x2 ; y2), alors $a=\frac{y_2–y_1}{x_2–x_1}$ et b = y1 – ax1 (ou b = y2 – ax2).

• graphiquement, en lisant le coefficient directeur a et l’ordonnée à l’origine b.

1 Déterminer la fonction affine associée à une droite (AB)

Considérons les deux points A(–1 ; 2) et B(3 ; 0) d’un repère du plan. Déterminer la fonction affine f dont la représentation graphique est la droite (AB).

Repère
Conseils

Calculez d’abord le coefficient directeur puis l’ordonnée à l’origine.

solution

On sait que, pour tout x, la fonction f est de la forme f(x) = ax + b.

De plus, grâce aux points A et B, on sait que : 2 = f(–1) et 0 = f(3).

Donc $a=\frac{2–0}{–1–3}=\frac{2}{–4}=–\frac{1}{2}$.

On trouve b en résolvant $0=a\times 3+b\Rightarrow –\frac{3}{2}+b=0\Rightarrow b=\frac{3}{2}$.

Conclusion : $f\left(x\right)=–\frac{1}{2}x+\frac{3}{2}$.

2 Déterminer le sens de variation et le signe d’une fonction affine

On considère les deux fonctions affines f et g ainsi définies : f(x) = 1 – 2x et g(x) = 4x + 3.

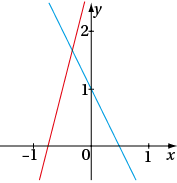
a. Associer chacune des droites ci-contre à sa fonction et indiquer leurs sens de variation respectifs.

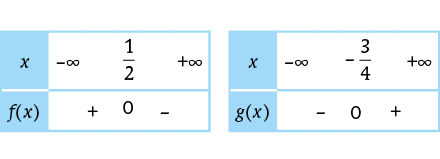
b. Dresser le tableau de signes de chacune d’elles.

Conseils

a. Déterminez les coefficients directeurs de chaque fonction.

b. Déterminez d’abord les nombres qui annulent chaque fonction.

solution

a. Le coefficient directeur de f est –2, négatif, et celui de g est 4, positif. Donc la fonction f est décroissante et g est croissante. Ainsi la droite bleue représente f et la droite rouge représente g.

b. Graphiquement ou algébriquement, on trouve ces ta­bleaux de signes.