Expression du produit scalaire dans un repère orthonormé

I. Propriété

Soit un repère orthonormé $(O, \overrightarrow{i}, \overrightarrow{j})$.

Si $\overrightarrow{u}(x ; y)$ et $\overrightarrow{v}(x' ; y')$ sont deux vecteurs, alors leur produit scalaire est donné par :

$\overrightarrow{u} \cdot \overrightarrow{v} = x x' + y y'$.

Démonstration

Dans un repère orthonormé, on a :

$||\overrightarrow{u}||^2 = x^2 + y^2$ et $||\overrightarrow{v}||^2 = x'^2 + y'^2$.

Leur somme est : $\overrightarrow{u} + \overrightarrow{v} = (x + x' ; y + y')$.

Donc : $||\overrightarrow{u} + \overrightarrow{v}||^2 = (x + x')^2 + (y + y')^2$.

D'après la formule du produit scalaire :

$\overrightarrow{u} \cdot \overrightarrow{v} = \dfrac{||\overrightarrow{u} + \overrightarrow{v}||^2 - ||\overrightarrow{u}||^2 - ||\overrightarrow{v}||^2}{2}$.

En remplaçant les normes :

$\overrightarrow{u} \cdot \overrightarrow{v} = \dfrac{(x + x')^2 + (y + y')^2 - x^2 - y^2 - x'^2 - y'^2}{2}$.

En développant :

$\overrightarrow{u} \cdot \overrightarrow{v} = \dfrac{x^2 + 2xx' + x'^2 + y^2 + 2yy' + y'^2 - x^2 - y^2 - x'^2 - y'^2}{2}$.

En simplifiant :

$\overrightarrow{u} \cdot \overrightarrow{v} = x x' + y y'$.

II. Orthogonalité de deux vecteurs

Définition

Deux vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$ sont orthogonaux lorsque : $\overrightarrow{u} \cdot \overrightarrow{v} = 0$.

Remarque

Le vecteur nul $\overrightarrow{0}$ est orthogonal à tous les vecteurs de l’espace, car pour tout vecteur $\overrightarrow{u}$ :

$\overrightarrow{u} \cdot \overrightarrow{0} = \overrightarrow{0} \cdot \overrightarrow{u} = 0$.

Propriété : Perpendicularité de deux droites

Deux droites sont perpendiculaires si et seulement si un vecteur directeur de l’une est orthogonal à un vecteur directeur de l’autre.

III. Un exemple

Dans le plan muni d’un repère orthonormé $(O ; \overrightarrow{i} ; \overrightarrow{j})$, on considère les points :

$A(-2 ; 0)$, $B(1 ; \sqrt{3})$, $C(-2 ; 2\sqrt{3})$.

$1.$ Calculer $||\overrightarrow{AB}||$, $||\overrightarrow{AC}||$ et $\cos(\overrightarrow{AB}, \overrightarrow{AC})$.

$2.$ En déduire la mesure principale de l’angle $(\overrightarrow{AB}, \overrightarrow{AC})$ puis la nature du triangle $ABC$.

Solution

$1.$ On a les vecteurs :

$\overrightarrow{AB}(3 ; \sqrt{3})$ et $\overrightarrow{AC}(0 ; 2\sqrt{3})$.

Donc : $||\overrightarrow{AB}|| = \sqrt{9 + 3} = \sqrt{12} = 2\sqrt{3}$.

Et : $||\overrightarrow{AC}|| = \sqrt{0 + 12} = 2\sqrt{3}$.

Le produit scalaire : $\overrightarrow{AB} \cdot \overrightarrow{AC} = 3 \times 0 + 2\sqrt{3} \times \sqrt{3} = 6$.

Or, d'après la définition du produit scalaire :

$\overrightarrow{AB} \cdot \overrightarrow{AC} = ||\overrightarrow{AB}|| \times ||\overrightarrow{AC}|| \times \cos(\overrightarrow{AB}, \overrightarrow{AC})$.

$= 2\sqrt{3} \times 2\sqrt{3} \times \cos(\overrightarrow{AB}, \overrightarrow{AC})$.

Ainsi : $12 \cos(\overrightarrow{AB}, \overrightarrow{AC}) = 6$.

Donc : $\cos(\overrightarrow{AB}, \overrightarrow{AC}) = \dfrac{6}{12} = \dfrac{1}{2}$.

$2.$ On sait que : \cos(\overrightarrow{AB}, \overrightarrow{AC}) = \dfrac{1}{2} > 0.

Cela signifie que : $(\overrightarrow{AB}, \overrightarrow{AC}) \in \left[ -\dfrac{\pi}{2} ; \dfrac{\pi}{2} \right]$.

Ainsi : $(\overrightarrow{AB}, \overrightarrow{AC}) = -\dfrac{\pi}{3}$ ou $(\overrightarrow{AB}, \overrightarrow{AC}) = \dfrac{\pi}{3}$.

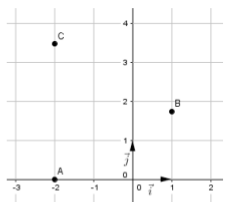
En plaçant les points dans un repère, on en déduit que : $(\overrightarrow{AB}, \overrightarrow{AC}) = \dfrac{\pi}{3}$.

Le triangle ABC est donc isocèle en $A$ et $(\overrightarrow{AB}, \overrightarrow{AC}) = \dfrac{\pi}{3}$.

On en déduit donc qu'il est équilatéral.