Evolution temporelle (ou cinétique) d'une transformation chimique

On supposera tout au long de cette fiche que le système étudié est fermé, de volume constant et de composition uniforme.

I. Transformations (ou réactions) rapides ou lentes

1. Transformations rapides

• Définition :

  Une transformation (ou réaction) rapide se fait quasi instantanément, dès que les réactifs sont en contact.

• Exemples :

  $\circ\quad$ Réaction entre $I_2$ et $S_2O_3^{2-}$ ;

  $\circ\quad$ Réaction entre $H_2O_2$ et $MnO_4^-$ en milieu acide.

2. Transformations lentes

• Définition :

  Une transformation (ou réaction) lente peut durer quelques minutes à plusieurs jours. Les produits ne se forment que progressivement.

• Exemple : réaction entre $I^-$ et $S_2O_8^{2-}$. Il se forme $I_2$ qui colore le mélange réactionnel en jaune puis brun de plus en plus foncé, au fur et à mesure que le temps passe.

3. Transformations infiniment lentes ou bloquées

• Définition :

  Le système chimique ne semble pas évoluer au cours du temps. La réaction peut durer plusieurs mois ou plusieurs années.

• Exemple : formation de la rouille.

4. Les facteurs cinétiques d'une transformation chimique

Pour plus de détails, lire la fiche suivante :

Les facteurs cinétiques d'une transformation chimique

5. Les catalyseurs d'une transformation chimique

Pour plus de détails, lire la fiche suivante :

Les catalyseurs d'une transformation chimique

II. Suivi de l'évolution temporelle d'une transformation chimique

1. Vitesse volumique d'une transformation

Définition :

À la date $t_1$, la vitesse volumique $v$ d'une transformation se déroulant dans un volume $V$ constant est la valeur de la dérivée par rapport au temps $t$ de l'avancement $x$ de la réaction, divisée par le volume $V$ :

$\boxed{v_{t_1} = \dfrac{1}{\text{V}} \cdot \left(\dfrac{\text{dx}}{\text{dt}}\right)_{t_{1}}}$

2. Détermination de la vitesse volumique d'une transformation

• Pratiquement, on ne dispose pas de la fonction $x(t)$. On a une série de points expérimentaux qui permettent de tracer la courbe $x = f(t)$.

• Propriété :

  La valeur de la dérivée par rapport au temps $t$ de l'avancement $x$, pour $t = t_1$, est donnée par le coefficient directeur de la tangente à la courbe $x = f(t)$ au point $A_1$ d'abscisse $t_1$.

• Rappel de mathématiques :

Ainsi on retiendra la formule suivante :

$v_{t_1} = \dfrac{1}{\text{V}} \times \text{coefficient directeur de la tangente de la courbe} ~~ x = f(t) ~~ \text{au point} ~ A_1 ~ \text{d'abscisse} ~~ t_1$

3. Évolution de la vitesse volumique d'une transformation

• Soit $t_2 \gt t_1$ et $\dfrac{1}{V} = \text{constante}$

• On constate dès lors que : coefficient directeur de ($T_2$) $\lt$ coefficient directeur de ($T_1$)

• Or, la vitesse volumique de la transformation peut s'écrire :

  $\circ\quad$ $v_{t_2} = \dfrac{1}{\text{V}} \times \text{coefficient directeur de} ~ T_2$ ;

  $\circ\quad$ $v_{t_1} = \dfrac{1}{\text{V}} \times \text{coefficient directeur de} ~ T_1$.

• Finalement, $\boxed{v_{t_2} \lt v_{t_1}}$.

• Propriété :

  Au fur et à mesure que le temps passe, la tangente à la courbe $x = f(t)$ se couche de plus en plus sur l'horizontale. Ainsi son coefficient directeur diminue et donc la vitesse volumique de la transformation diminue.

4. Évolution des concentrations des réactifs et des produits

• Considérons la transformation suivante : $\boxed{\alpha A + \beta B \longrightarrow \gamma C + \delta D}$.

• On établit le tableau d'avancement de cette transformation :

• A un instant $t$, les quantités de matière des réactifs disparaissant et des produits apparaissant s'expriment en fonction de l'avancement $x$ de cette réaction :

  $\circ\quad$ $n(A) = n_i(A) - \alpha \cdot \text{x} \Leftrightarrow x = \dfrac{n_i(A) - n(A)}{\alpha}$ ;

  $\circ\quad$ $n(B) = n_i(B) - \beta \cdot \text{x} \Leftrightarrow x = \dfrac{n_i(B) - n(B)}{\beta}$ ;

  $\circ\quad$ $n(C) = n_i(C) + \gamma \cdot \text{x} \Leftrightarrow x = \dfrac{n(C) - n_i(C)}{\gamma}$ ;

  $\circ\quad$ $n(D) = n_i(D) + \delta \cdot \text{x} \Leftrightarrow x = \dfrac{n(D) - n_i(D)}{\delta}$.

• Or, par définition de la vitesse volumique de la transformation : $v_t = \dfrac{1}{\text{V}} \cdot \dfrac{d\text{x}}{d\text{t}}$

  $\circ\quad$ Pour le $\textcolor{purple}{\text{réactif A}}$ :

  $v_t = \dfrac{1}{\text{V}} \cdot \dfrac{d\left(\frac{n_i(A) - n(A)}{\alpha}\right)}{d\text{t}} = - \dfrac{1}{\alpha} \cdot \dfrac{d\left(\frac{n(A)}{V}\right)}{dt} = - \dfrac{1}{\alpha} \cdot \dfrac{d [A]}{dt}$

  si $[A]$ est la concentration en quantité de matière de $A$ à l'instant $t$ ;

  $\circ\quad$Pour le $\textcolor{orange}{\text{réactif B}}$, on peut également démontrer que : $v_t = - \dfrac{1}{\beta} \cdot \dfrac{d [B]}{dt}$

  si $[B]$ est la concentration en quantité de matière de $B$ à l'instant $t$ ;

  $\circ\quad$Pour le $\textcolor{green}{\text{réactif C}}$, on peut aussi démontrer que : $v_t = + \dfrac{1}{\gamma} \cdot \dfrac{d [C]}{dt}$

  si $[C]$ est la concentration en quantité de matière de $C$ à l'instant $t$ ;

  $\circ\quad$Pour le $\textcolor{blue}{\text{réactif D}}$, on peut enfin démontrer que : $v_t = + \dfrac{1}{\delta} \cdot \dfrac{d [D]}{dt}$

  si $[D]$ est la concentration en quantité de matière de $D$ à l'instant $t$.

• Vitesses d'apparition et de disparition :

  Les vitesses de disparition des réactifs s'écrivent :

  $\circ\quad$ $\boxed{v_A(t) = - \dfrac{d[A]}{dt}}$ pour le réactif $A$ ;

  $\circ\quad$ $\boxed{v_B(t) = - \dfrac{d[B]}{dt}}$ pour le réactif $B$.

  Les vitesses d'apparition des produits s'écrivent :

  $\circ\quad$ $\boxed{v_C(t) = + \dfrac{d[C]}{dt}}$ pour le produit $C$ ;

  $\circ\quad$ $\boxed{v_D(t) = + \dfrac{d[D]}{dt}}$ pour le produit $D$.

• Exemple : réaction entre $I^-$ et $S_2O_8^{2-}$

  $\circ\quad$ On mélange une solution $(K^+ + I^-)$ de concentration $C_1$ et de volume $V_1$ avec une solution $(2Na^+ + S_2O_8^{2-})$ de concentration $C_2$ et de volume $V_2$.

  $\circ\quad$ L'équation de la réaction lente étudiée est $2I^- + S_2O_8^{2-} \longrightarrow I_2 + 2SO_4^{2-}$.

  $\circ\quad$ On peut éventuellement tracer un tableau d'avancement de cette réaction lente.

  $\circ\quad$ Ici, l'avancement de la réaction est $x = n(I_2)$ et $[I_2] = \dfrac{n(I_2)}{V}$ = concentration molaire du diiode dans le mélange réactionnel si $V = V_1 + V_2$ = volume du mélange réactionnel = constante.

  $\circ\quad$ Finalement, $\displaystyle \left(\dfrac{d\text{x}}{d\text{t}}\right)_{t_{1}} = \left(\dfrac{d~\text{n}(I_{2})}{d\text{t}}\right)_{t_{1}} = \left(\dfrac{d([I_2] \cdot \text{V})}{d\text{t}}\right)_{t_{1}}$

  $\circ\quad$ Or $V = \text{constante}$, d'où

  $\Longrightarrow v_{t_1} = \displaystyle \dfrac{1}{\text{V}} \cdot \text{V} \cdot \left(\frac{d[I_{2}]}{d\text{t}}\right)_{t_{1}}$

  $\Longrightarrow v_{t_1} = \displaystyle \left(\dfrac{d[I_{2}]}{d\text{t}}\right)_{t_{1}}$

• Conclusion : la vitesse volumique de cette transformation à la date $t_1$ est la valeur de la dérivée de la concentration molaire du diiode par rapport au temps $t$.

III. Temps de demi-réaction et loi de vitesse d'ordre 1

1. Notion de temps de demi-réaction

Définition :

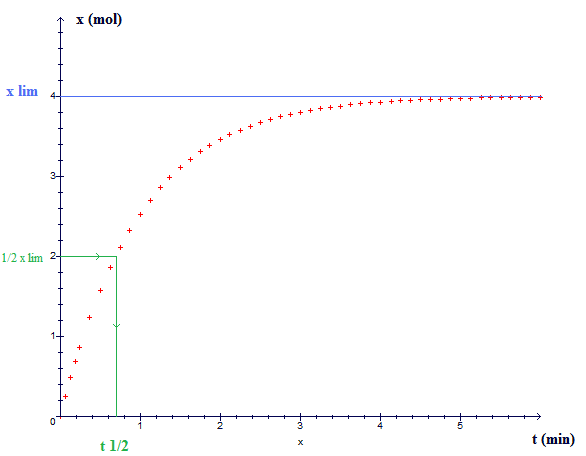
Le temps de demi-réaction, noté $t_{\frac{1}{2}}$, est la durée nécessaire pour que l'avancement $x$ de la réaction soit égal à la moitié de sa valeur limite.

$\boxed{\text{x} \left(t_{\frac{1}{2}} \right) = \dfrac{1}{2} \cdot \text{x}_{\text{limite}}}$

2. Détermination pratique du temps de demi-réaction

On lit la courbe $x = f(t)$ si la réaction est totale $x_{\text{limite}} = x_{\text{max}}$.

3. Loi de vitesse d'ordre 1

• Énoncé de la loi :

  Pour des transformations dites d'ordre $1$ par rapport à un réactif $X_i$, la vitesse volumique de disparition de cette espèce est proportionnelle à sa concentration en quantité de matière :

  $\boxed{v_{X_i} = k \times [X_i]}$

  $\circ\quad$ $v_{X_i}$ est la vitesse de disparition du réactif $X_i$ ($mol.L^{-1}.s^{-1}$) ;

  $\circ\quad$ $k$ constante de vitesse ($s^{-1}$) ;

  $\circ\quad$ $[X_i]$ concentration en quantité de matière du réactif $X_i$ ($mol.L^{-1}$).

• Remarques :

  $\circ\quad$ La courbe représentant la vitesse de disparition de $X_i$ en fonction de sa concentration en quantité de matière est alors une droite passant par l'origine ;

  $\circ\quad$ Le temps de demi-réaction d'une transformation d'ordre $1$ ne dépend que de la constante de vitesse $k$ : elle ne dépend donc pas de la concentration en quantité de matière initiale du réactif $X_i$.

_{= Merci à gbm pour avoir contribué à l'élaboration de cette fiche =}