Équations et fonctions polynômes du second degré

On fait le lien entre les fonctions polynômes du second degré et le produit de deux fonctions affines. Ce qui permet d’étudier leur signe à l’aide de tableaux de signes.

I. Définitions

Une fonction polynôme du second degré à coefficients réels est une fonction P, définie sur ℝ, telle qu’il existe trois réels a, b et c avec a ≠ 0, et telle que pour tout réel x, P(x) = ax² + bx + c.

Les réels a, b et c sont appelés les coefficients de P (a en est le coefficient domi­nant).

Soit a, b et c des réels tel que a ≠ 0. L’équation ax² + bx + c = 0 est appelée équation du second degré.

Une racine du polynôme P(x) = ax² + bx + c est une solution de l’équation ax² + bx + c = 0.

II. Produit de deux fonctions affines et étude de signe

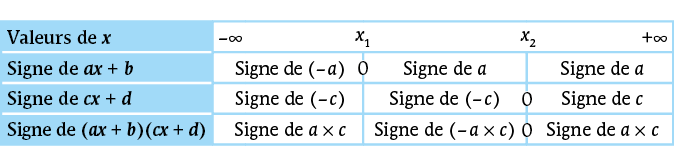
1)  Produit de fonctions affines

Soit a, b, c et d des réels tels que a ≠ 0 et c ≠ 0, alors le produit des deux ­fonctions affines x ↦ (ax + b)(cx + d) est une fonction polynôme du second degré.

Ses racines x1 et x2 sont –ba et –dc.

Son signe est résumé dans le tableau de signes.

2)  Identités remarquables

Pour tous réels a et x, on a :

• x² + 2ax + a² = (x + a)² ;

• x² – 2ax + a² = (x – a)² ;

• x² – a² = (x + a)(x – a).

À noter

Deux fonctions polynômes du second degré sont égales si et seulement si elles ont les mêmes coefficients.

Méthode

Déterminer les racines et le signe d’un produit de fonctions affines

Résoudre l’équation (1 – 4x)(3x + 2) = 0 puis l’inéquation (1 – 4x)(3x + 2) < 0.

Repère

Conseil

• Pour résoudre une équation-produit, on s’assure tout d’abord qu’elle est bien de la forme f(x) × g(x) = 0. On identifie ensuite chacun des facteurs, puis on résout chacune des équations obtenues.

On rappelle le théorème suivant : un produit de facteurs est nul si et seulement si un des facteurs est nul.

• Pour résoudre une inéquation de la forme f(x) × g(x) > 0 ou f(x) × g(x) < 0, on détermine tout d’abord le signe de chacun des facteurs puis on dresse un tableau de signes du produit.

Solution

On a pour tout réel x :

(1 – 4x)(3x + 2) = 0 ⇔ 1 – 4x = 0 ou 3x + 2 = 0

⇔ 1 = 4x ou 3x = –2

⇔ x=14 ou x=–23.

Ainsi, l’équation (1 – 4x)(3x + 2) = 0 admet pour seules solutions 14 et .

On a le tableau de signes suivant :

On en déduit que l’inéquation (1 – 4x)(3x + 2) < 0 admet pour solutions les réels appartenant à ]–∞ ;–23[∪]14;+∞[.

À noter

Soit m et p deux réels, m ≠ 0 ; le signe de la fonction x ↦ mx + p est déterminé par le signe de m et par sa racine –pm : si m > 0, la fonction est négative puis positive ; si m < 0 la fonction est positive puis négative.