L’effet Joule se manifeste dans tous les composants électriques qui possèdent une résistance interne et qui sont parcourus par un courant électrique.
I. Dipôle ohmique
1) Loi d’Ohm pour un dipôle ohmique
Un dipôle ohmique est caractérisé par sa résistanceR en ohms (Ω).
La relation entre la tension U aux bornes du dipôle ohmique et l’intensité du courant I qui le parcourt est la loi d’Ohm :
À noter
En convention « récepteur », U et I sont de sens opposés.
La caractéristique U = f(I) est donc une droite passant par l’origine dont le coefficient directeur est R.
2) Loi de Joule
L’énergie électrique consommée par le dipôle ohmique pendant la durée de fonctionnement Δt est EJ=U×I×Δt=R×I2×Δt=U2R×Δt, soit une puissance consommée : PJ=R×I2=U2R.
L’énergie électrique consommée est dissipée sous forme thermique : c’est l’effet Joule. Il y a échauffement du dipôle ohmique et transfert thermique vers l’extérieur.
II. Avantages et inconvénients de |’effet Joule
L’effet Joule est « utile » dans les dispositifs destinés à fournir de l’énergie sous forme thermique tels que les appareils de chauffage (radiateurs, bouilloire…), les dispositifs de sécurité (disjoncteur thermique, coupe-circuit…).
Souvent, l’effet Joule n’est pas désiré, car il provoque un échauffement inutile et une « perte » d’énergie pour l’utilisateur (ordinateurs, moteurs électriques…).
Méthodes
1) Déterminer la caractéristique d’un dipôle ohmique
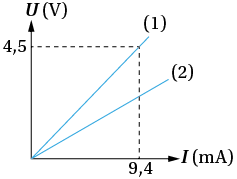
On donne ci-contre les caractéristiques intensité-tension de deux dipôles ohmiques de résistances respectives R1, pour la droite (1), et R2, pour la droite (2).
a. Calculer la valeur de la résistance R1
b. Déterminer, sans calcul, quelle est la valeur de résistance la plus grande entre R1 et R2.
Conseils
a. Déterminez la pente (ou le coefficient directeur) de la droite (1).La pente d’une droite passant par l’origine se détermine avec les coordonnées de deux points de la droite dont l’un est l’origine.
b. Comparez les pentes des deux droites.
Solution
a. La loi d’Ohm s’écrit U = R × I ainsi R représente la pente de la droite passant par l’origine U = f(I). On a : R=UI. Sur la droite (1), on choisit le point (9,4 mA ; 4,5 V) d’où : R1=4,59,4×10–3=4,8×102 Ω.
b. R représente la pente de la droite U = f(I). Or des droites (1) et (2), la droite la plus pentue est la droite (1). Donc R1 > R2.
2) Appliquer la loi de Joule
Un fer à repasser de résistance R = 50 Ω est traversé par un courant d’intensité I = 4,6 A. Calculer la valeur :
a. de la puissance dissipée par effet Joule ;
b. de l’énergie dissipée par effet Joule pour une durée Δt = 30 min de repassage.
Conseils
b. Faites le lien entre puissance et énergie.
Solution
a. La puissance dissipée par effet Joule s’écrit : PJ = R × I2.
Application numérique : PJ = 50 × 4,62 = 1,1 × 103 W = 1,1 kW.
b. L’énergie dissipée par effet Joule se calcule par : EJ = PJ × Δt.
Application numérique : EJ = 1,1 × 103× 30 × 60 = 1,9 × 106 J = 1,91 MJ.