Tout comme les nombres entiers relatifs, les nombres à virgule peuvent aussi être représentés en base 2.
I. Conversion de la base 2 à la base 10
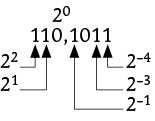
Les chiffres à gauche de la virgule correspondent à des puissances de 2 positives, ceux situés à droite correspondent à des puissances de 2 négatives.
Exemple :
On a donc
II. Conversion de la base 10 vers la base 2
Commencer par convertir la partie entière.
Pour convertir la partie décimale, procéder par multiplications par 2 successives. Après chaque multiplication le résultat est reporté sans sa partie entière. Le calcul se poursuit jusqu’à ce qu’on obtienne 1.
Exemple :
III. Écritures infinies
Certains nombres ont une écriture décimale infinie périodique (par exemple 711=0,636363…). Et certains ont une écriture binaire infinie périodique, alors même que leur écriture décimale est finie.
Exemple :
À noter
De tous les nombres ne comportant qu’un seul chiffre après la virgule en base 10, seul 0,5 a une écriture binaire finie.
IV. Codage des nombres à virgule
1) Virgule fixe et virgule flottante
Il existe deux codages des nombres à virgule en machine : le codage en virgule fixe, et le codage en virgule flottante (norme IEEE-754, existant en simple, double ou quadruple précision).
Le codage en virgule fixe est encore utilisé dans certains microcontrôleurs. Le codage en virgule flottante est utilisé partout ailleurs : ordinateurs, smartphones…
L’idée du codage en virgule fixe est de retenir un nombre fixe de chiffres après la virgule.
Dans le cas du codage en virgule flottante, on retient un nombre fixe de chiffres significatifs (beaucoup de chiffres après la virgule pour les petits nombres, et beaucoup de chiffres avant la virgule pour les grands nombres).
2) Les nombres à virgule sont approchés
Quel que soit le codage choisi, le problème est le même : si le nombre a une écriture infinie en base 2, il ne peut pas être représenté dans un ordinateur qui ne stocke qu’un nombre fini de chiffres et utilise la base 2. Le nombre manipulé sur machine n’est alors qu’une valeur approchée du nombre réel.
C'est le cas avec tous les langages qui utilisent les nombres à virgule flottante (c’est-à-dire à peu près tous les langages qui ne sont pas spécialisés dans le calcul exact).
Exemple : Le calcul 0,5 – 0,2 – 0,2 – 0,1 ne donne généralement pas 0.
Ajouter un petit nombre à un grand donne des résultats surprenants :
Exemple :
L’addition avec des flottants n’est plus commutative :
Exemples :