Célérité d’une onde et retard

Les vagues à la surface de l’eau, une mélodie chantonnée ou une secousse sismique se propagent avec une célérité qui leur est propre et dépend de leur milieu de propagation.

I. Célérité d’une onde

La vitesse de propagation d’une onde est appelée célérité, et est notée v. On détermine la célérité d’une onde par le quotient de la distance d parcourue par l’onde pendant une durée de propagation Δt :

À noter

La célérité du son est plus importante dans les solides que dans les gaz.

La célérité dépend de la nature de l’onde et du milieu de propagation.

Exemple : quelques valeurs de célérité du son

II. Retard au cours de la propagation d’une onde

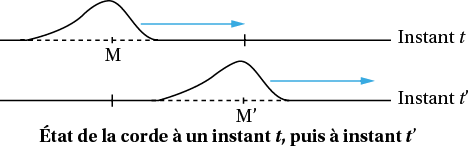
Lorsqu’une onde se propage, les différents points du milieu sont atteints par la perturbation à des dates différentes. Si on considère deux points distincts M et M′ du milieu de propagation, la perturbation passe d’abord en M à l’instant t, puis en M′ à l’instant t′.

L’instant ultérieur t′ est lié à l’instant antérieur t par la relation suivante : t′ = t + τ. Cela revient à dire que le point M’ subit la même perturbation que le point M avec un retard égal à : τ = t′ – t. Le retard au passage de l’ondeτen M′ correspond au temps mis par l’onde pour parcourir la distance MM′ avec une célérité v :

Méthode

Déterminer la célérité d’une onde mécanique

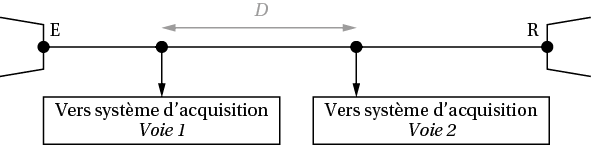
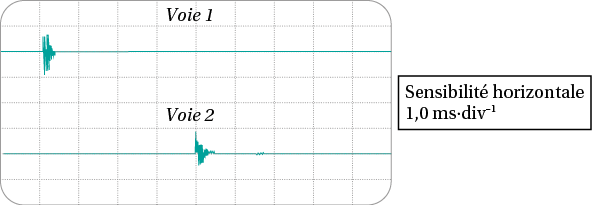
Pour déterminer la célérité de l’onde le long d’une corde, on place sur la corde deux capteurs distants de : D = 32,0 cm et reliés à un système informatisé d’acquisition de données. On réalise l’enregistrement suivant.

a. Déterminer le retard de l’onde entre les deux détecteurs.

b. Exprimer la célérité v de l’onde en fonction de la distance D et du retard τ.

c. Calculer cette célérité.

Conseils

a. Le retard est un décalage temporel entre les deux détections. La sensibilité horizontale fournit la valeur en temps d’une division de l’écran.

b. Rappelez-vous de la formule du cours.

c. Pensez à convertir. L’unité de la célérité est le mètre par seconde. Les conversions suivantes doivent être connues : 1 ms = 1  × 10⁻³ s et 1 cm = 1  × 10⁻² m.

Solution

a. Entre les deux voies de mesure, on compte quatre divisions de décalage temporel. En tenant compte de la sensibilité horizontale, on trouve : τ = 4 × 1,0 = 4,0 ms.

b. On utilise la formule du retard pour trouver v : τ=Dv d’où v=Dτ.

c. On applique la formule de v en ayant réalisé les conversions d’unité ­adéquates : v=0,3204,0×10–3=80 m ⋅s–1.