Arguments d'un complexe non nul

Dans tout ce qui suit, le plan est rapporté à un repère orthonormé direct $(0\;; \vec u \;,\vec v)$

I. Mesures d'un angle orienté

Cas particulier :

Si $M'$ est le point image du réel $x$, alors une mesure de l’angle orienté $(\overrightarrow{u}, \overrightarrow{OM})$ est $x$.

Remarque :

Un angle orienté a une infinité de mesures.

Si $\theta$ est l’une d’entre elles, alors $\theta + 2k\pi$ avec $k \in \mathbb{Z}$ est aussi une mesure de l’angle orienté.

On notera donc : $(\overrightarrow{w_1} ; \overrightarrow{w_2}) = \theta [2\pi]$.

Exemple :

$(\overrightarrow{u} ; \overrightarrow{v}) = \dfrac{\pi}{2} [2\pi]$

$(\overrightarrow{v} ; \overrightarrow{u}) = -\dfrac{\pi}{2} [2\pi]$

II. Définition des arguments d'un complexe non nul

Soit $z$ un nombre complexe non nul et $M$ le point d’affixe $z$.

Un argument de $z$ est une mesure en radians de l’angle $\widehat{(\overrightarrow {u}\;; \overrightarrow{OM})}$. On le note $\arg(z)$.

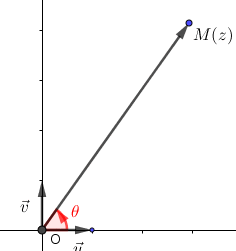
Notation : Un nombre complexe a une infinité d’arguments. Si $\theta$ est un argument de $z$, on notera : $\arg(z) = \theta [2\pi]$.

Exemple :