Le théorème de Thalès : propriétés et réciproque avec exemples
Le théorème de Thalès est l’un des deux grands théorèmes du collège avec le théorème de Pythagore que tu as dû déjà voir. Le théorème, ainsi que la réciproque, vont te permettre de calculer des longueurs et de montrer que des droites sont parallèles (ou non). Focus sur tous les éléments à retenir du théorème de Thalès.

SOMMAIRE
Le théorème de Thalès, c’est quoi ?
Quand l’appliquer ?
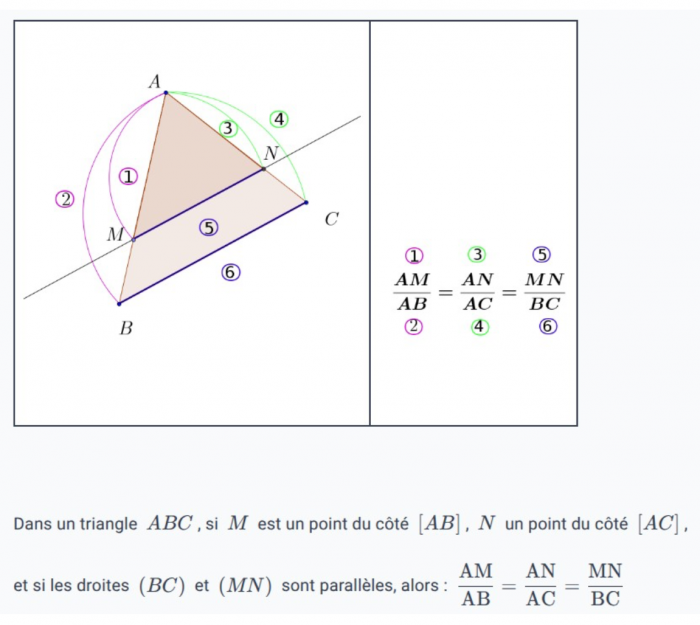
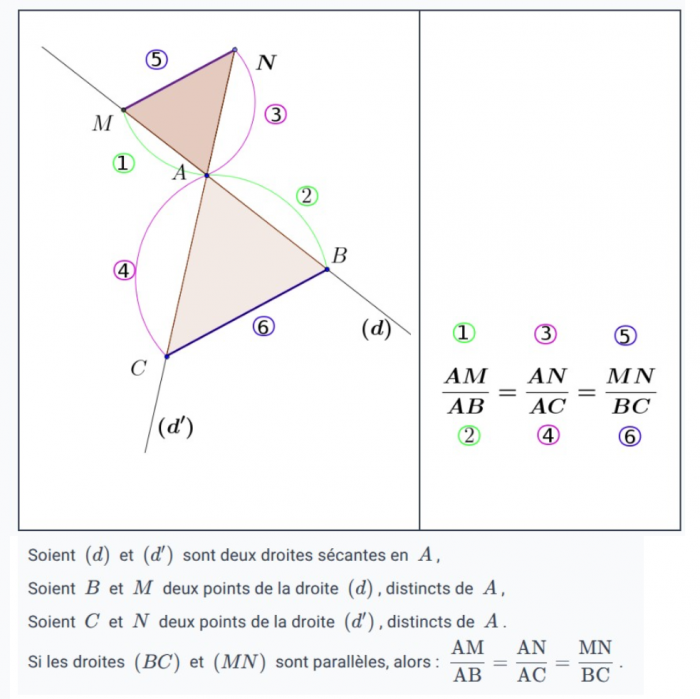
Le théorème de Thalès s’applique dans deux configurations distinctes, mais les formules vont être les mêmes. Quand on coupe deux droites sécantes par deux droites parallèles, on obtient deux triangles. Ces triangles peuvent être « l’un dans l’autre » (ils sont dits emboîtés) ou en forme de sablier (ils sont dits en forme de papillon également) :

Réciproque du théorème de Thalès
La réciproque du théorème de Thalès permet de démontrer que des droites sont parallèles.
Exemple :

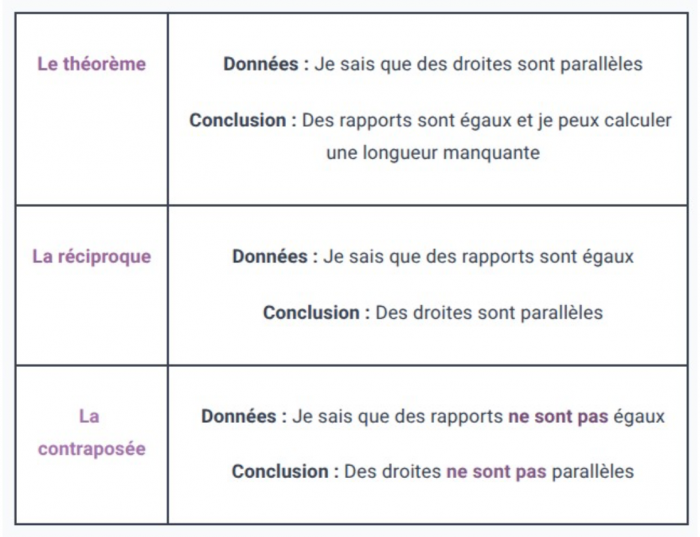
Conséquence du Théorème de Thalès : la contraposée du théorème de Thalès
Le théorème de Thalès permet aussi de montrer que deux droites ne sont pas parallèles (par l’absurde) en montrant qu’il n’y a pas d’égalité, on parlera de contraposée du théorème de Thalès.
Si deux triangles sont formés par deux droites sécantes d’une part, et deux autres droites, et si les côtés associés ne sont pas proportionnels, alors les deux autres droites ne sont pas parallèles.
Ceci est une conséquence du théorème de Thalès, comme l’égalité n’est pas vérifiée, c’est que les droites ne sont pas parallèles.


En résumé :