Le théorème de Pythagore : méthodes, formules, réciproque avec exemples

SOMMAIRE

• Définition
• Résoudre un problème
• Réciproque

Qu’est-ce que le théorème de Pythagore ?

Le théorème de Pythagore est une propriété qui permet de calculer la longueur du troisième côté, l’hypoténuse, d’un triangle rectangle lorsque les deux autres côtés sont connus. 

La propriété énoncée est la suivante : si un triangle est rectangle, alors le carré du plus long côté, l’hypoténuse, est égal à la somme des carrés des deux autres côtés.

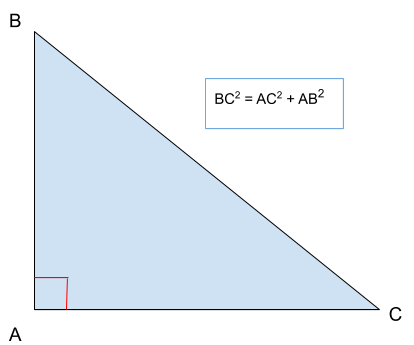
Formulation équivalente : si le triangle ABC est rectangle en A alors BC² = AC² + AB².

Ainsi, dans un triangle rectangle, le carré de l’hypoténuse est égal à la somme des carrés des côtés de l’angle droit.

Exemples

1°) Soit un triangle ABC rectangle en A et tel que AB = 15 cm et BC = 18,75 cm. On veut calculer la mesure exacte de la distance AC. 

[AB] et [AC] sont les côtés de l’angle droit, [BC] est l’hypoténuse.

Nous pouvons appliquer le théorème de Pythagore et écrire : BC² = AB² + AC².

Alors AC² = BC² − AB² ou encore AC² = 18,752−152.
Donc AC² = 126,5625, soit AC = 11,25 cm.

2°) On veut calculer un des côtés de l’angle droit.

Soit DEF un triangle rectangle en D. On donne DF = 6 cm et EF = 9 cm. Calculer DE.

DEF est un triangle rectangle en D.

D’après le théorème de Pythagore, on a :
DF² = DE² + EF²
9² = DE² + 6²

Soit 81 = DE² + 36 ⇔ 81 – 36 = DE² = 45 

Ainsi DE ≃ 6,7 cm

Découvre également notre cours de 3ᵉ sur le théorème de Pythagore.

Résoudre un problème à l’aide du théorème de Pythagore

Deux chemins rectilignes D1 et D2 se coupent perpendiculairement en O. Deux très bons marcheurs P1 et P2 partent simultanément du point O et prennent chacun un des deux chemins à vitesse constante : v1=2 m/s pour P1 et v2=2,5 m/s pour P2.

Calculer la distance séparant les deux marcheurs 600 secondes après leur départ. En donner une valeur approchée au mètre près.

Au bout de 600 secondes, P1 sera en A avec OA =2×600 =1 200 m et P2 sera en B avec OB = 2,5 × 600 =1 500 m.

Le triangle OAB est rectangle en O.

Le théorème de Pythagore permet d’écrire : AB² = OA² + OB².

AB² = 1 200² + 1 500² = 3 690 000,

soit AB² = 3 690 000.

Nous obtenons AB = 1 921 m, valeur approchée au mètre près.

Remarque

Le théorème de Pythagore est particulièrement utile pour calculer des longueurs qu’on ne peut pas mesurer, comme des grandes distances sur la Terre ou dans l’espace (astronomie).

Réciproque

La réciproque du théorème de Pythagore est une propriété qui permet de dire si un triangle est rectangle ou non lorsqu’on connaît les longueurs de ses 3 côtés.

La propriété est la suivante : Si le carré de la longueur du plus grand côté d’un triangle est égal à la somme des carrés des longueurs de ses deux autres côtés, alors ce triangle est rectangle et admet pour hypoténuse le plus grand des côtés.

Autrement dit, si un triangle ABC est tel que BC² = AB² + AC², alors ce triangle est rectangle en A.

Exemple

Soit un triangle ABC tel que AB = 5,7cm ; AC = 8,4 cm et BC = 10cm. Le triangle est-il rectangle ?

1. [BC] est le plus grand des côtés du triangle ABC.

2. Calculons : AB² = 5,72= 32,49 ; AC² = 8,42 = 70,56 ; BC² = 102 = 100.

3. Puisque 32,49 + 70,56 = 103,05, alors 32,49 + 70,56 ≠ 100.

Par conséquent : AB² + AC² ≠ BC².

Conclusion : Si le triangle ABC avait été rectangle en A, alors nous aurions pu appliquer le théorème de Pythagore et écrire que AB² + AC² = BC². Mais AB² + AC² ≠ BC², donc le triangle ABC n’est pas rectangle en A.