Cette fiche aborde la propriété de la somme des angles d’un triangle qui est importante pour déterminer la mesure d’un angle.
I) La leçon
1) Inégalité triangulaire
Dans un triangle, la longueur d’un côté (en particulier le plus grand) est toujours strictement inférieure à la somme des longueurs des deux autres côtés.
Cela permet de savoir si un triangle existe lorsqu’on donne la longueur de ses trois côtés. (voir Ce qu’il faut savoir faire ci-dessous).
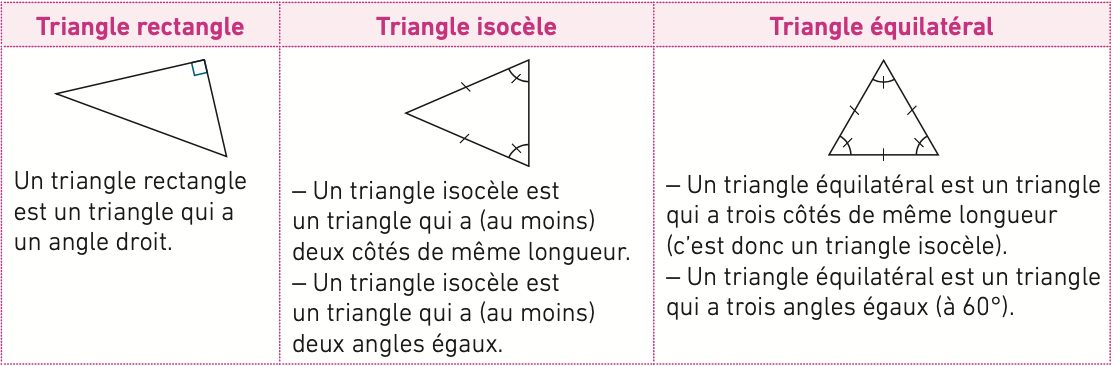
2) Triangles particuliers
Ces propriétés sont dites « caractéristiques », c’est-à-dire qu’elles permettent de démonter qu’un triangle est particulier (rectangle, isocèle ou équilatéral) et, s’il est particulier, d’en déduire les propriétés sur les angles et les longueurs de côté.
Un triangle peut être rectangle et isocèle.
Un triangle qui n’est ni rectangle, ni isocèle (donc ni équilatéral) est un triangle quelconque.
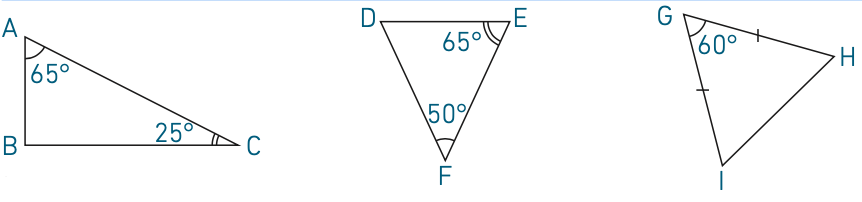
3) Somme des angles d’un triangle
Propriété : dans un triangle, la somme des angles est égale à 180°.
II) Ce qu'il faut savoir faire
Tracer un triangle dont on donne les longueurs des trois côtés
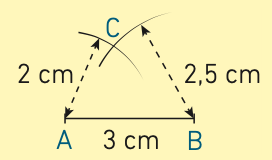
Exemple : tracer si possible un triangle ABC tel que AB = 3 cm, AC = 2 cm et BC = 2,5 cm.
• Étape 1 : AB est le plus grand côté et AB < AC + BC donc le triangle est constructible.
• Étape 2 : On trace un des côtés.
• Étape 3 : Avec le compas on trace le troisième sommet. • On trace les deux autres côtés.
Attention : le tracé consistant à faire des essais avec sa règle pour placer le troisième sommet ne convient pas. Il faut laisser les traits de construction (arcs de cercle) qui attestent que le compas a été utilisé.
Calculer un angle en utilisant la propriété de la somme des angles d’un triangle
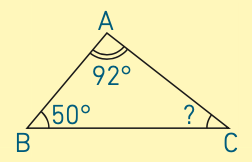
Exemple : calculer l’angle du triangle ACB.
Démontrer qu’un triangle est rectangle ou isocèle ou équilatéral en utilisant la somme des angles d’un triangle
Exemple : ABC est un triangle tel que = 47° et = 43°. Démontrer que ABC est un triangle rectangle.
On utilise la propriété caractéristique des angles de ces triangles particuliers. Dans le triangle ABC, on a = 180° − (47° + 43°) = 90° donc ABC est un triangle rectangle en C.
III) Je m'entraine
1. a. Tracer si possible un triangle KLM tel que KL = 4 cm, LM = 5 cm et KM = 3 cm.
b. Tracer si possible le triangle NPR tel que NR = 6 cm NP = 8 cm et PR = 1,5 cm.
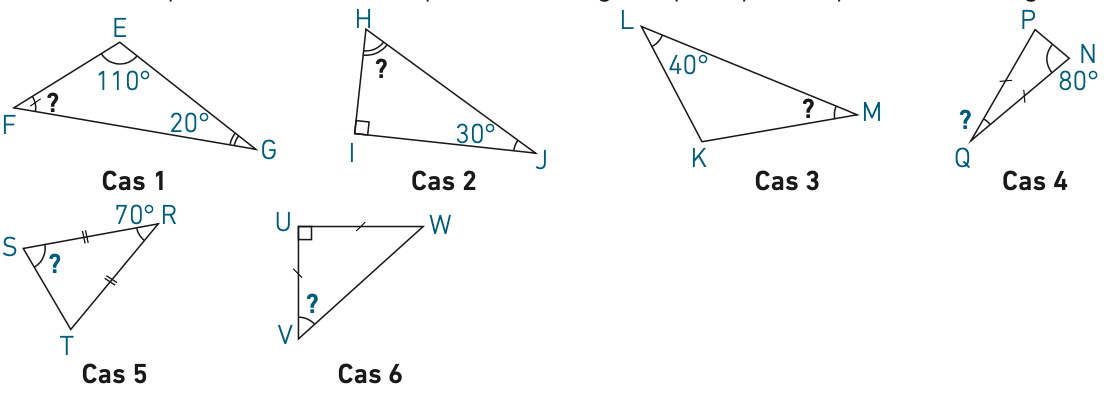
2. Dans chaque cas, calculer, si possible, l’angle repéré par un point d’interrogation.
3. Déterminer, de la façon la plus précise possible, la nature de chacun de ces triangles.