Droites et angles

Plusieurs propriétés lient les droites et les angles et permettent de calculer des angles et de démontrer que des droites sont parallèles.​

I) La leçon

1) Angles opposés par le sommet

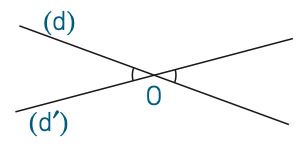
Deux angles opposés par le sommet sont deux angles qui ont un sommet commun et dont les côtés sont dans le prolongement l’un de l’autre.

Propriété 1 : deux angles opposés par le sommet sont égaux.

Les angles 1 et 2 sont opposés par le sommet.

2) Angles alternes-internes, correspondants

a. Définition

Les angles alternes-internes et correspondants sont définis par deux droites et une sécante à ces deux droites.

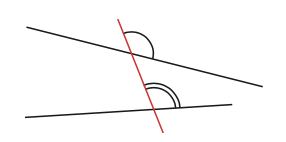
Angles alternes-internes

Les angles alternes-internes sont « entre » les deux droites et de part et d’autre de la sécante.

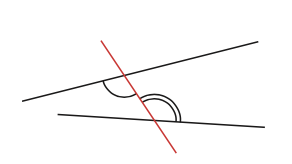
Angles correspondants

Les angles correspondants sont situés du même côté de la sécante. L’un est « entre » les deux droites et l’autre est à « l’extérieur ».

b. Propriétés

Propriété 2 : des angles alternes-internes (ou correspondants) formés par des droites parallèles sont égaux.

Propriété 3 : si des angles alternes-internes (ou correspondants) sont égaux, alors ils sont formés par des droites parallèles.

• Les propriétés 1 et 2 permettent de démontrer que des angles sont égaux et donc de déterminer la mesure d’angles.

• La propriété 3 permet de démontrer que des droites sont parallèles.

II) Ce qu'il faut savoir faire

Reconnaitre des angles alternes-internes, correspondants

Déterminer la mesure d’angles en utilisant les propriétés des angles opposés par le sommet, alternes-internes et correspondants

Démontrer que des droites sont parallèles en utilisant les propriétés des angles alternes-internes et correspondants

III) Je m'entraine

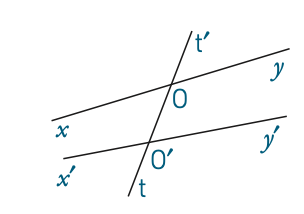
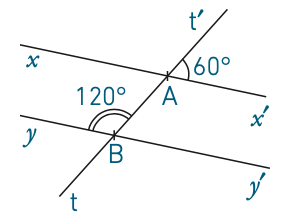
1. En utilisant la figure ci-dessus, compléter :

a. Les angles $\widehat{x\text{Ot}}$ et ... sont correspondants.

b. Les angles $\widehat{\text{t'O}y}$ et ... sont opposés par le sommet.

c. Les angles $\widehat{y'\text{O't'}}$ et ... sont alternes-internes.

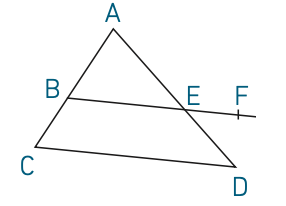
2. En utilisant les lettres figurant sur le dessin ci-dessous, nommer tous les angles opposés par le sommet, et tous les angles alternes-internes et correspondants.

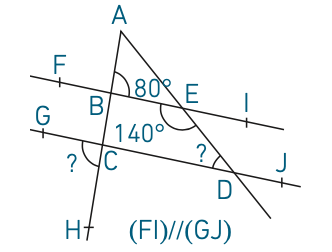
3. Calculer les angles marqués par un point d’interrogation.

4. Démontrer que les droites ($xx'$) et ($yy'$) sont parallèles.