Un système de numération est un ensemble de symboles (les chiffres) et de règles qui permettent d’écrire les nombres entiers naturels.

I) Leçon

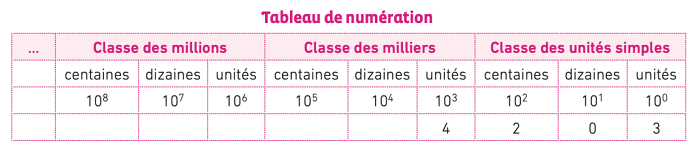
1) Système de numération de base dix

$\rightarrow$ Dans le système de base dix (système de numération décimale), les nombres entiers naturels sont écrits à l’aide de dix chiffres (0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 et 9).
$\rightarrow$ Ce système est décimal (il évoque des groupements successifs de dix éléments) et positionnel (la valeur d’un chiffre est déterminée par son rang).

Rappel : $b^{0}=1$ et $b^{n}=\underbrace{b\times b\times \ldots \times b}_{n\rm\ \text{facteurs égaux à}\rm\ \textit{b}}$

2) Chiffres des... et nombre de...

En base dix, un nombre entier naturel peut être décomposé à l’aide des puissances de 10.
Exemple 1 : $4~203=4\times10^3+2\times10^2+3\times10^0$

Dans 4 203, 4 est le chiffre des milliers, 2 le chiffre des centaines...
Exemple 2 : en base dix, le nombre 4 203 peut aussi être décomposé sous d’autres formes.
$4~203=42\times10^2+3\times10^0$
Cette décomposition met en évidence que, dans 4 203, 42 est le nombre de centaines.
$4~203=420\times10^1+3\times10^0$
Cette décomposition met en évidence que, dans 4 203, 420 est le nombre de dizaines.

3) Système de numération de base b

$\rightarrow$ Dans un système de base b (b entier naturel, b>1), les nombres entiers naturels sont écrits à l’aide de b chiffres : 0, 1, ... à $b-1$ .
$\rightarrow$ Ce système est fondé sur des groupements successifs de b éléments et il est positionnel (la valeur d’un chiffre est déterminée par son rang).
$\rightarrow$ b étant un entier naturel supérieur à 1, tout nombre entier naturel n peut être décomposé à l’aide des puissances de b :

Par exemple, ici, $n=a_{3}\times b^3+a_{2}\times b^2+a_{1}\times b^1+a_{0}\times b^0$ où $a_{3} ; a_{2} ; a_{1} ; a_{0}$ sont tous des entiers naturels inférieurs à b. On écrit : $n=\overline{a_{3}a_{2}a_{1}a_{0}}^{\text{base}\rm\ \textit{b}}$ .

II) Ce qu'il faut savoir faire

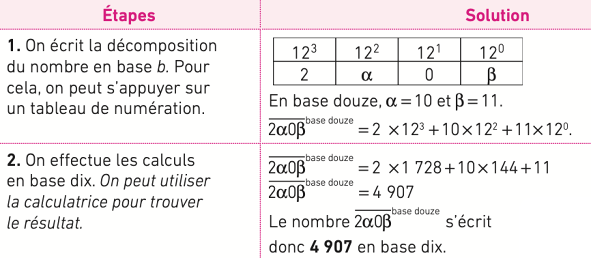
$\rightarrow$ Écrire en base dix un nombre donné en base b
Exemple : écrire en base dix le nombre $\overline{2\alpha0\beta}^\text{base douze}$ , les chiffres en base douze étant successivement 0, 1, 2... 9, α, β.

$\rightarrow$ Écrire en base b un nombre donné en base dix
Exemple : écrire en base quatre le nombre 147 (donné en base dix).

III) Je m'entraîne

1. Écrire en base dix le nombre $\overline{4~021}^\text{base cinq}$ .
2. Écrire en base six le nombre 445 donné en base dix.